Solve Disc/Shell Problem: Find Volume of Solid Revolved Around x=6

[xyzyx]

I'm pretty new to discs/shells and I'm having a hard time with it. Here's a problem I've been stuck on for a few days now:

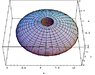
I need to find the volume of a solid by revolving the region bounded on the left by x = y^2 +1 and by x = 5 on the right side. It is revolved around x = 6.

My work (I can't figure out how to make it appear as it would in the book, so I apologize if this becomes confusing):

I took the integral from -2 to 2 of (pi) times (6 - (y^2 +1))^2.

int from -2 to 2 ((pi) (5-y^2)^2) dy

(pi) int from -2 to 2(25 - 10 y^2 + y^4) dy

(pi) ((25y - (10y^3/3) + (y^5/5) from -2 to 2)

(pi) ((50 - (80/3) + (32/5)) - (-50 + (80/3) - 32/5))

(pi) (100 - (160/3) + (64/5))

(pi) ((1500/15) - (800/15) + (192/15))

= 892(pi)/15

I tried using the shell method but that turned out even worse, so I figure I'm supposed to use the disc method.

Any help or tips?

 

[incognitO]

First write the area of the anular region from the disk with radius 1 centered in $x=6$ to $x=y^2+1$, then integrate over the whole height of the figure (a drawing will make it clearer).

EDIT:

Hah, that's exactly what you did... assuming your calculation is good, then ur all set!

 

[xyzyx]

Well, I'm pretty sure I did all the calculations correct; it was just a matter of setting up the problem correctly (I always have a hard time with that part lol).

Thanks for confirming my work!

 

[Dale]

Your limits of integration are correct, since +/-2 is where the line intersects the parabola. So, basically you are trying to find the volume of something that looks kind of like a donut, but with a sharp edge around the "hole". The way to find the volume is to imagine you are slicing it into thin disks, you find the area of each disk and integrate it over your +/-2 range. The area of each disk is the area of a circle with radius given by the parabola ($$\pi \,{\left( 6 - (y^2 + 1) \right) }^2$$) minus the area of a circle with radius given by the line ($$\pi \,{\left( 6 - 5 \right) }^2$$).

You will use the disc method to calculate volumes and the shell method to calculate surface areas. With the disk method you integrate areas to get volumes and with the shell method you integrate lengths to get areas.

By the way, I think the only mistake that you made is that your integrand should be $$\pi \,\left( 24 - 10\,y^2 + y^4 \right)$$ instead of $$\pi \,\left( 25 - 10\,y^2 + y^4 \right)$$. I think that mistake came from forgetting to subtract out the area of the hole.

-Hope that helps
Dale

 

[xyzyx]

Heh, I guess I spoke too soon.

I'm still a little fuzzy on why it's 24 and not 25. First, I foiled (5 - y^2)^2 to get 25 - 10y^2 + y^4. Do I subtract 1 from the 25 because it's bounded by x = 5 and is revolved around x = 6, therefore giving it a difference of 1?

If that's how it goes then I completely understand it now.

 

[Dale]

Heh, I guess I spoke too soon.
I'm still a little fuzzy on why it's 24 and not 25. First, I foiled (5 - y^2)^2 to get 25 - 10y^2 + y^4. Do I subtract 1 from the 25 because it's bounded by x = 5 and is revolved around x = 6, therefore giving it a difference of 1?
If that's how it goes then I completely understand it now.

Yes, that is correct. There is a hole of radius 1 in your object since it is bounded by x=5 and revolved around x=6. That is why I think it is useful to try and picture in your mind what the object looks like, in this case kind of like a donut with a sharp edge around the hole. So the math to get the area of the disk for the integrand goes something like this:
$$\pi \,{r_{out}}^2 - \pi \,{r_{in}}^2$$
$$\pi \,{\left( 6 - (y^2 + 1) \right) }^2) - \pi \,{\left( 6 - 5 \right) }^2$$
$$\pi \,\left( 25 - 10\,y^2 + y^4 \right) - \pi \,1$$
$$\pi \,\left( 24 - 10\,y^2 + y^4 \right)$$

-Dale