Solve Disk & Coil Spring Motion: Get Amplitude Help

[Lil123]

Homework Statement

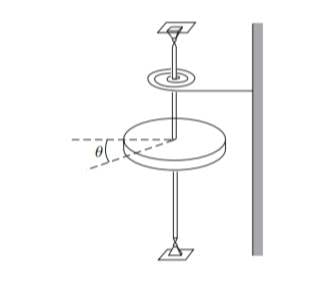
A solid disk of mass M and Raduis R is on vertical .The shaft is
attached to a coil spring that exact a linear restoring torque of magnitude C theta where theta is the angle measured from the static equilibrium position in C is a constant neglect the mass of the shaft and the spring and assume the bearing to be frictionless.




1.Show that the disk and undergo simple harmonic motion motion and find the frequency frequency of the motion


2.Suppose that the disc is moving according to theta equals to theta not sin omega t where Omega is the frequency found in part a at time T1 equals to pi by Omega a ring of sticky putty of mass M and radius R is dropped cocentrically on the disc find the new amplitude of the motion

Relevant Equations

Li =Lf

I was able to solve part 1 but I am not

not getting how to find new amplitude of the motion . Please help me

 

[haruspex]

2.Suppose that the disc is moving according to theta equals to theta not sin omega t where Omega is the frequency found in part a at time T1 equals to pi by Omega a ring of sticky putty of mass M and radius R is dropped cocentrically on the disc find the new amplitude of the motion

Took me a while to decode that. Do you mean
"Suppose that the disc is moving according to $\theta=\theta_0\sin (\omega t )$ where ω is the frequency found in part 1.
"At time $T_1 = \pi /\omega$ a ring of sticky putty of mass M and radius R is dropped concentrically on the disc. Find the new amplitude of the motion."
?

For part 2, you need to show an attempt. You have quoted the relevant equation. Can you fill in the details for this context?

 

[Lil123]

This is the above question. How do I find new amplitude of the motion ?

 

[haruspex]

This is the above question. How do I find new amplitude of the motion ?

Using your conservation of angular momentum equation.
What is the total angular momentum of the system just before the putty hits the disc? So what is the angular speed just after?

 

[Lil123]

Using your conservation of angular momentum equation.
What is the total angular momentum of the system just before the putty hits the disc? So what is the angular speed just after?

Yes , but how do I find angular speed ? .I know angular frequency of the system before and after the putty hits the disc

 

[haruspex]

Yes , but how do I find angular speed ? .I know angular frequency of the system before and after the putty hits the disc

You can find the angular speed before the collision either from energy conservation or from the given equation of motion.

 

[Lnewqban]

...
2.Suppose that the disc is moving according to theta equals to theta not sin omega t where Omega is the frequency found in part a at time T1 equals to pi by Omega a ring of sticky putty of mass M and radius R is dropped cocentrically on the disc find the new amplitude of the motion
Relevant Equations: Li =Lf

I was able to solve part 1 but I am not View attachment 328105not getting how to find new amplitude of the motion . Please help me

If mass is added to the moving system, but not additional energy to do the work, how things must naturally change to adjust to the increased inertia and still move under the influence of the same elastic energy?

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html

 

[haruspex]

the same elastic energy?

Mechanical energy is not conserved here. @Lil123 quoted the relevant equation.