Solve for H/L Ratio in Equal Tetrahedron

[chmilne]

Here's the problem:

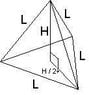
A regular tetrahedron is a three-dimensional object that has four faces, each of which is an equilateral triangle. Each of the edges of such an object has a length L. The height H of a regular tetrahedron is the perpendicular distance from one corner to the center of the opposite triangular face. Show that the ratio between H and L is H/L = sqrt (2/3).

Here's what I've done so far:
Take a look at the attachment.

L2 = H2 + (H/2)2
L2 = H2 + (H2/2)
L2 = ( (2H2)/2 ) + (H2/2)
L2 = 3H2/2
2L2 = 3H2
(√2)L = (√3)H
((√2) / (√3)) / L = H
((√2) / (√3)) = H / L
√(2/3) = H / L

I was excited that I thought I had found the answer that I completely squared the 'b' in this euqation, thus throwing off the rest of the equation. I know I'm close, but I seem to be missing something. Will someone please help?

 

[Integral]

Show me that the base of the triangle is $\frac h 2$

Please take the time to read https://www.physicsforums.com/showthread.php?t=8997". Your equations are not very clear.

 

[danago]

Im finding it kinda hard to understand your working, but shouldn't the second line be:
L2 = H2 + (H2/4)
?

 

[HallsofIvy]

The center of an equilateral triangle is on the altitude, 1/3 of the way from the vertex to the base. That is not "H/2". If an equilateral triangle has sides of length L, what is the length of the altitude? What is 1/3 of that?

 

[Robokapp]

In an equilateral triangle the Height is always side times sq(3)/2, that's basic Geometry knowledge, but do you mean the height of the whole figure, or the height of one of the faces? That...is not the same.