Solve for ##x## in an equation involving surds

[chwala]

Homework Statement

see attached

Relevant Equations

quadratic/cubic equations

Kindly see the questions and its mark scheme below;

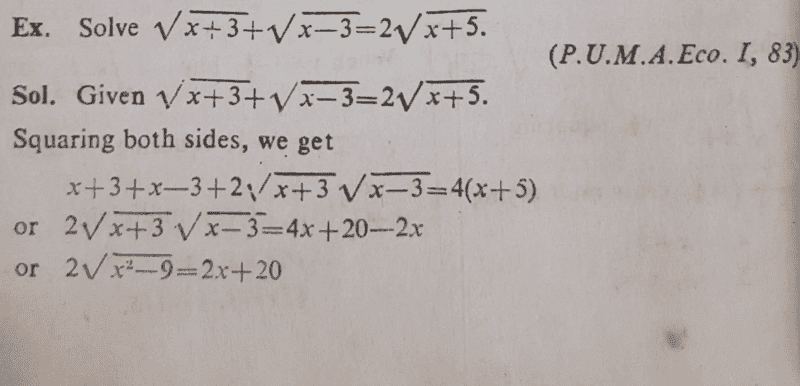
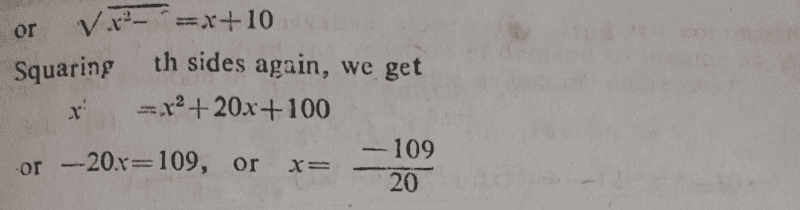
This is well understood. I was trying to look at the problem from a different perspective. (see attached below my attempt);

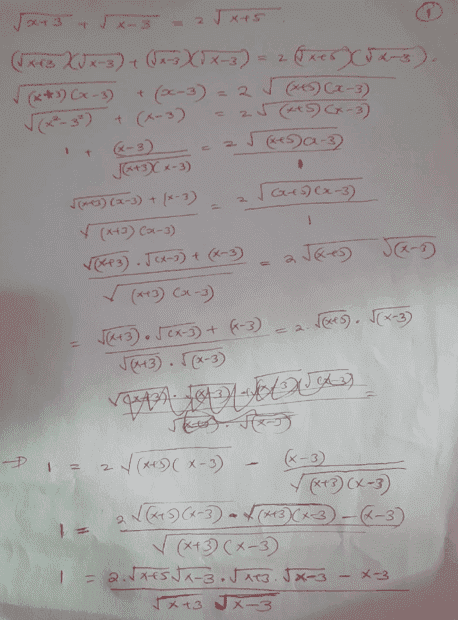
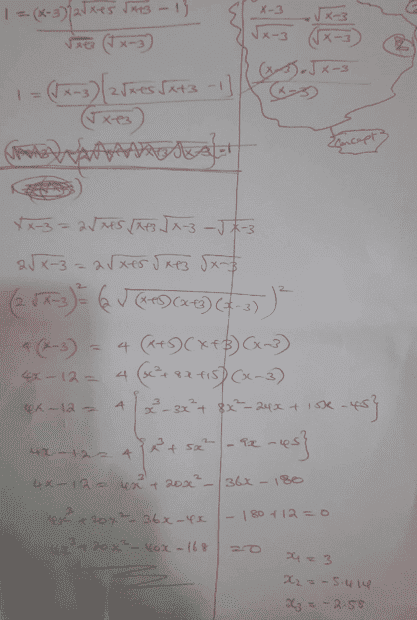
Makes any sense? cheers...

ok i can see some mistake...i will amend it later...let me amend it first then you guys can chime in later..

...I seem to be going round in circles...looks like squaring both sides would realize what we want...

 

[PeroK]

Assuming we are looking for real solutions, we have:
$$\sqrt{x + 3} < \sqrt {x + 5} \ \text{and} \ \sqrt{x - 3} < \sqrt {x + 5}$$ $$\sqrt {x + 3} + \sqrt {x - 3} < 2\sqrt{x + 5}$$Hence, there are no real solutions.

The proposed solution $x = -\frac{109}{20}$ leads to the equation:
$$\sqrt{-49} + \sqrt{-169} = 2\sqrt{-9}$$ Which only works if we take:
$$\sqrt{-49} = -7i, \ \sqrt{-169} = 13i, \ \sqrt{-9} = 3i$$

 

[chwala]

Assuming we are looking for real solutions, we have:
$$\sqrt{x + 3} < \sqrt {x + 5} \ \text{and} \ \sqrt{x - 3} < \sqrt {x + 5}$$ $$\sqrt {x + 3} + \sqrt {x - 3} < 2\sqrt{x + 5}$$Hence, there are no real solutions.

The proposed solution $x = -\frac{109}{20}$ leads to the equation:
$$\sqrt{-49} + \sqrt{-169} = 2\sqrt{-9}$$ Which only works if we take:
$$\sqrt{-49} = -7i, \ \sqrt{-169} = 13i, \ \sqrt{-9} = 3i$$

$√(-49=±7i$ & $√(-69)=±13i$...in this case do we only consider the values that satisfy the equation, like you have rightly indicated?

 

[PeroK]

$√(-49=±7i$ & $√(-69)=±13i$...in this case do we only consider the values that satisfy the equation, like you have rightly indicated?

No, square roots are uniquely defined. The solution in the book is wrong. What they showed was that IF the equation has a solution, then that solution is $-\frac{109}{20}$. But, they didn't check that really is a solution. Note that squaring both sides of an equation gives a one-way implication, as a solution of the squared equation may not be a solution of the original equation.

If you are considering real numbers, then any solution must be $\ge 3$ in any case.

You could patch up the origin equation by changing it to:$$-\sqrt {z + 3} + \sqrt {z - 3} = 2\sqrt{z + 5}$$And then $z = -\frac{109}{20}$ is a solution.

 

[chwala]

No, square roots are uniquely defined. The solution in the book is wrong. What they showed was that IF the equation has a solution, then that solution is $-\frac{109}{20}$. But, they didn't check that really is a solution. Note that squaring both sides of an equation gives a one-way implication, as a solution of the squared equation may not be a solution of the original equation.

If you are considering real numbers, then any solution must be $\ge 3$ in any case.

You could patch up the origin equation by changing it to:$$-\sqrt {z + 3} + \sqrt {z - 3} = 2\sqrt{z + 5}$$And then $z = -\frac{109}{20}$ is a solution.

that's true, the equation can only have real roots with $x$ being in the domain, $x≥3$

 

[kumusta]

that's true, the equation can only have real roots with $x$ being in the domain, $x≥3$

If the equation referred to above is
(1)$\qquad–~\sqrt {z + 3}~+ \sqrt {z - 3} = 2\sqrt {z + 5}~$
that could have only real roots $~z = x~\geq~3~$, then why does $~z = x = 4~\gt~3~$give for the left-hand side of (1)
$\qquad{~~~~}–~\sqrt {4 + 3}~+ \sqrt {4 - 3} = –\sqrt 7 + 1 = –2.6 + 1 = –1.6$
whereas from the right-hand side, we find
$\qquad{~~~~}2\sqrt {4 + 5} = 2\sqrt 9~= 6~\ne~–1.6$
Since the equality in (1) is not satisfied, then $~x≥3~$ does not give the roots of (1) rewritten in the form
(2)$\qquad\sqrt {z + 3}~- \sqrt {z - 3}~+ 2\sqrt {z + 5} = 0$
The only root of (2) is $~\frac {–~109}{20}~$ which has zero imaginary part so there's really no need to use a complex variable but simply write (1) as
$\qquad{~~~~}–~\sqrt {x + 3}~+ \sqrt {x - 3} = 2\sqrt {x + 5}~$.

 

[chwala]

I do not know whether we are talking on the same problem, Looking at the problem; Solve
$√(x+3) +√(x-3)=2√(x+5)$, then $x$ can only be defined in the domain $x≥3$, that's what i meant. Any other value less than $3$ would realize a complex form of solution...of course if i did not get it right then do correct me...

...you slightly altered the original equation, hence use of the term 'if'

 

[PeroK]

I do not know whether we are talking on the same problem ...

There's a subtlety here. If we write $$f(x) = \sqrt {x - 3}$$then this could mean one of two functions:
$$f: [3, \infty) \rightarrow \mathbb R$$Or:
$$f: \mathbb R \rightarrow \mathbb C$$Strictly speaking, therefore, we cannot allow $x < 3$ without admitting complex numbers at least implicitly. Although, it's true that we could retain the real numbers as the domain of our function.

 

[kumusta]

If the problem is to find a real root of the equation
(1)$\qquad~\sqrt {x+3} + \sqrt {x-3} - 2√(x+5) = 0$
then clearly, $~x~\geq~3$. But if the aim is to find the general root of (1), not just the real root, then obviously complex roots must be admissible..