Solve Force on Square Loop with Current I in Non-Uniform Field

[stunner5000pt]

Homework Statement

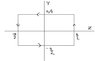
Problem 5.4 Suppose that the magnetic field in some region has the form $B=kz \hat{x}$ where k is a constant). Find the force on a square loop (side a), lying in the yz plane and centered at the origin, if it carries a current I, flowing counterclockwise, when you look down the x axis.

Homework Equations

$$\vec{F} = I \int d\vec{l} \times \vec{B}$$

The Attempt at a Solution

Now i can easily prove that the forces in the two sides that are in line with tehe Y axis cancel out

For the segments parallel to the Z axis however things are a bit different
on the top segment for z>0
$$F = i \frac{a}{2} k \frac{a}{2} (\hat{-z}\times\hat{x}) = \frac{ika^2}{4} \hat{y}$$
For the bottom segment z>0
$$F = i \frac{a}{2} k \frac{a}{2} (\hat{z}\times\hat{x}) = -\frac{ika^2}{4} \hat{y}$$

For the top segment z<0
$$F = i \frac{a}{2} k \frac{-a}{2} (\hat{-z}\times\hat{x}) = -\frac{ika^2}{4} \hat{y}$$
For the bottom segment z<0
$$F = i \frac{a}{2} k \frac{-a}{2} (\hat{z}\times\hat{x}) = \frac{ika^2}{4} \hat{y}$$

but don't all these forces just cancel to zero??

where have i gone wrong?? I know the answer can't be zero because this is not a uniform field...

Thanks for your help!

(edit: i have changed the diagram since i had done it wrong, the current should have been in the opposite direction)

 

[Meir Achuz]

The forces on the top wire and the bottom wire are in the same direction.
z is only >0 for the top wire and only <0 for the bottom wire.
z can't be <0 at the topp wire.
There are only two forces to add.

 

[stunner5000pt]

The forces on the top wire and the bottom wire are in the same direction.
z is only >0 for the top wire and only <0 for the bottom wire.
z can't be <0 at the topp wire.
There are only two forces to add.

why can't z <0 for hte top wire... doesn't part of the wire lie in the z<0 region? And isn't the field different in taht region aswell??

 

[Doc Al]

Now i can easily prove that the forces in the two sides that are in line with tehe Y axis cancel out

Sure about that?

but doesn't the left side of the loop lie in the z<0 part of the YZ plane? Thus, doesn't the magnetic field become negative??

Yes.

 

[stunner5000pt]

Sure about that?

on second thought... it doenst cancel out

for hte right side loop
$$F = i \frac{a}{2} \hat{y} \times k \frac{a}{2} \hat{x} = \frac{ika^2}{4} \hat{z}$$

$$F = i \frac{a}{2} (-\hat{y}) \times k \frac{-a}{2} \hat {x} = \frac{ika^2}{4} \hat{z}$$

so the force points to the right, according to my diagram and has value $$\vec{F} = \frac{ika^2}{2} \hat{z}$$thanks a lot!

 

[Brown Arrow]

The forces on the top wire and the bottom wire are in the same direction.
z is only >0 for the top wire and only <0 for the bottom wire.
z can't be <0 at the topp wire.
There are only two forces to add.

when i do the Right hand rule i see that on top force is up and at bottom its down so they cancel
now the sides the force also points in opposite direction so they cancel...
this does not make sense to me at all could some1 explain please

 

[ideasrule]

when i do the Right hand rule i see that on top force is up and at bottom its down so they cancel
now the sides the force also points in opposite direction so they cancel...
this does not make sense to me at all could some1 explain please

Are you sure you got the directions of the magnetic field right? To summarize, if k>0, the field points up on the right side of the image and down on the left side.