MHB Solve Functions Question: Speed/Distance/Time & Composition

[MarkFL]

Here is the question:

HELP WITH THIS FUNCTIONS QUESTION!?

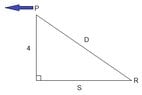
An airplane passes directly over a radar station at time t = 0. The plane maintains an altitude of 4km and is flying at a speed of 560km/hr. Let D represent the distance from the radar station to the plane, and let S represent the horizontal distance traveled by the plane since it passed over the radar station.

---

a) Express D as a function of S, and S as a function of T
b) Use composition to express the distance between the plane and the radar station as a function of time.
c) How far from the station is the plane 10 minutes later?

Here is a link to the question:

HELP WITH THIS FUNCTIONS QUESTION!? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Hello sorry lads,

For the given questions, please refer to the following diagram (all linear measures are in km):

https://www.physicsforums.com/attachments/848._xfImport

The plane is at point $P$ and the radar station is at point $R$.

a) Express $D$ as a function of $S$, and $S$ as a function of $t$.

To express $D$ as a function of $S$, we may observe that the Pythagorean theorem allows us to write:

$$S^2+4^2=D^2$$

Now, taking the positive root since lienar measures are taking to be non-negative, we have:

$$D(S)=\sqrt{S^2+4^2}$$

To express $S$ as a function of $t$, we may use the fact that for constant speed, distance is speed times time elapsed. For now, we will let the positive constant $v$ represent the speed of the plane, and we have:

$$S(t)=vt$$

b) Use composition to express the distance between the plane and the radar station as a function of time.

$$D(t)=D(S(t))=\sqrt{(vt)^2+4^2}$$

As you can see, we merely need to substitute $S(t)$ for $S$ in $D(S)$ to get $D(t)$

c) How far from the station is the plane 10 minutes later?

Since time is in hours (to be consistent with $v$ which is in kph), this means:

$$t=10\text{ min}\cdot\frac{1\text{ hr}}{60\text{ min}}=\frac{1}{6}\,\text{hr}$$

Using the given value of $$v=560\,\frac{\text{km}}{\text{hr}}$$

we then find:

$$D\left(\frac{1}{6}\,\text{hr} \right)=\sqrt{\left(560\,\frac{\text{km}}{\text{hr}}\cdot\frac{1}{6}\,\text{hr} \right)^2+(4\text{ km})^2}=\sqrt{\left(\frac{280}{3} \right)^2+4^2}\text{ km}=\frac{4}{3}\sqrt{4909}\,\text{km}\approx93.41900829655124\text{ km}$$

To sorry lads and any other guests viewing this topic, I invite and encourage you to post other algebra questions here in our http://www.mathhelpboards.com/f2/ forum.

Best Regards,

Mark.