- #1
Lizu
- 3
- 1
hi! i need help for this inequality
1. ##a\in\mathbb{N}*~and~ \frac{a}{a+1}<\frac{a+1}{a+2}<\frac{a+2}{a+3}##
show that : ##\frac{1}{2}*\frac{4}{5}*...*\frac{2005}{2006}*\frac{2008}{2009}<\frac{1}{12}##
Here i have stoped. Please tell me if is corect what i have done so far and how to continue , or another idea to solve
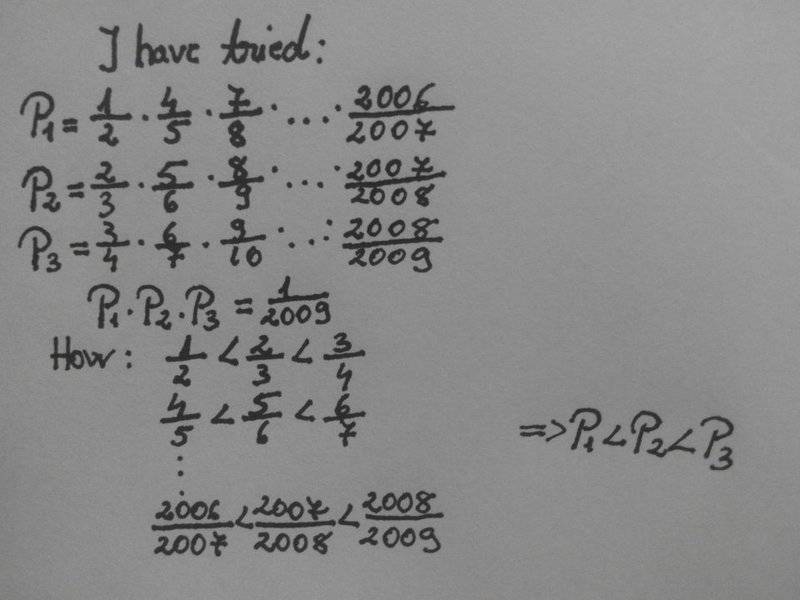
1. ##a\in\mathbb{N}*~and~ \frac{a}{a+1}<\frac{a+1}{a+2}<\frac{a+2}{a+3}##
show that : ##\frac{1}{2}*\frac{4}{5}*...*\frac{2005}{2006}*\frac{2008}{2009}<\frac{1}{12}##
Here i have stoped. Please tell me if is corect what i have done so far and how to continue , or another idea to solve
