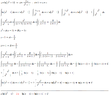Solve Integral of ln(x^2-1) with Ease: Step-by-Step Guide

[Yankel]

Hello all,

I am trying to solve this integral,

\[\int \ln(x^{2}-1) \, dx\]

but I get stuck no matter what I do, if I go for substitution or parts...

thanks

 

[Ackbach]

Here's a hint: $x^2-1=(x+1)(x-1)$.

 

[Yankel]

Ok, I tried your suggestion, and I did this, however, it is the wrong answer...

\[\int ln((x-1)(x+1))dx=\int (ln(x-1)+ln(x+1))dx=\]

\[=\int ln(x-1)dx+\int ln(x+1)dx=\]

\[\int ln(u)du+\int ln(t)dt=(x-1)ln(x-1)+(x+1)ln(x+1)-2x+C\]

The correct answer should be:

\[xln(x^{2}-1)-2x-ln\left | x-1 \right |+ln\left | x+1 \right |+C\]

 

[Chris L T521]

Ok, I tried your suggestion, and I did this, however, it is the wrong answer...

\[\int ln((x-1)(x+1))dx=\int (ln(x-1)+ln(x+1))dx=\]

\[=\int ln(x-1)dx+\int ln(x+1)dx=\]

\[\int ln(u)du+\int ln(t)dt=(x-1)ln(x-1)+(x+1)ln(x+1)-2x+C\]

The correct answer should be:

\[xln(x^{2}-1)-2x-ln\left | x-1 \right |+ln\left | x+1 \right |+C\]

I would approach it in the following manner: first apply integration by parts to get

\[\begin{aligned} \int \ln(x^2-1)\,dx &= x\ln(x^2-1) - \int\frac{2x^2}{x^2-1}\,dx\\ &= x\ln(x^2-1)-\int 2+\frac{2}{x^2-1}\,dx\end{aligned}\]

and then use the hint Ackbach gave you.

Can you take things from here? (Smile)

 

[Yankel]

Integration by parts and then use the method of fractions ?

still, I am curious to know what I did wrong earlier...

 

[Chris L T521]

Integration by parts and then use the method of fractions ?

still, I am curious to know what I did wrong earlier...

The problem is in claiming that $\ln(x^2-1) = \ln(x-1)+\ln(x+1)$. The property $\ln(ab)=\ln(a)+\ln(b)$ can only be applied when $a>0$ and $b>0$! However, we see that the domain of $\ln(x^2-1)$ is $(-\infty,-1)\cup(1,\infty)$ but the domain of $\ln(x-1)+\ln(x+1)$ is $(1,\infty)$, so we see now that they're not necessarily the "same function"; it's just a portion of $\ln(x^2-1)$. In fact,

\[\ln(x^2-1) = \begin{cases} \ln(x-1)+\ln(x+1) & x>1\\ \ln(1-x) + \ln(-x-1)& x<-1\end{cases}\]

In essence, what you found was $\displaystyle\int \ln(x^2-1)\,dx$ under the constraint that $x>1$. You didn't find $\displaystyle\int \ln(x^2-1)\,dx$ such that it was defined for any $x\in(-\infty,-1)\cup(1,\infty)$. Approaching it by parts and then partial fractions will get you the antiderivative that the solution is looking for.

I hope this made sense (I'm rather tired, so I'm not sure my explanation/reasoning was good enough).

 

[Yankel]

Thank you for your help, I understand my mistake.

I tried the way you suggested, and I got something very similar to the answer I look for, however one item is missing.

My solution is attached, my final answer is in bold. Underneath, in red, the real answer according to the book and maple.

I can't find my current mistake either...

View attachment 2025

 

[Ackbach]

Your mistake is in the partial fraction decomposition. It is not true that
$$ \frac{1}{2(x-1)}- \frac{1}{2(x+1)}= \frac{x^{2}}{(x-1)(x+1)}.$$
Just get the common denominator and check it out. Instead, you have
$$\frac{1}{2(x-1)}- \frac{1}{2(x+1)}= \frac{1}{(x-1)(x+1)}.$$
You have to perform polynomial long division first, as Chris mentioned, before you can do the partial fraction decomposition. Indeed, your equation $x^2=A(x+1)+B(x-1)$ should have clued you in that there was a problem: there are no $A$ and $B$ that can make the equation work, because on the LHS you have a quadratic, but no quadratic powers on the RHS.