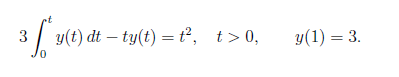Solve integral with laplace transform

[goohu]

So the task is to solve the following integral with laplace transform.
View attachment 9423

Since t>0 we can multiply both sides with heaviside stepfunction (lets call it \theta(t)).

What I am unsure about is what happens with the integral part and how do we inpret the resulting expression?

What will it result in and how will be laplace transform the integral parts? I am also wondering what the laplace transform of y(t) will be.

 

[Ackbach]

So you have the equation
$$ 3\int_0^t y(\tau)\,d\tau -t\,y(t)=t^2,\quad y(1)=3.$$
Here I've changed the variable of integration so it's less confusing. Now we take the Laplace Transform of the equation thus:
$$\frac{3Y(s)}{s}+Y'(s)=\frac{2}{s^3}. $$
This is now a differential equation in $s.$ It's first-order linear, so it should be pretty straight-forward to solve. Answer:
$$Y(s)=\frac{2}{s^2}+\frac{C}{s^3}. $$
Finally, the inverse transform yields
$$y(t)=2t+\frac{Ct^2}{2}. $$
Can you finish applying the initial condition, and checking that the solution works in the original integral equation?