Solve Magnetism Problem: Find Direction, Magnitude of Force

[doodijh]

Homework Statement

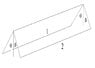
Two wires have a current going through them and each wire is suspended by a string from the ceiling.
Wire 2 makes an angle of β with the vertical and Wire 1 makes and angle of θ with the vertical.
(see the attached picture for further clarification)

L 1(length of wire) = ?
I 1(current) = ?
L 2(length of wire) = ?
I 2(current) = ?
B (magnetic field) =?
D (distance in between the two wires) =?
M1 (mass of wire 1) = ?
M2 = ?
Fm = ?

a) Find the direction of current in the two wires?
b) State the magnitude of the magnetic force between the two wires (1&2)?
c) Find the magnitude of the magnetic force in each wire?

Homework Equations

Current carrying wire in a magnetic field

Magnetic field due to current carrying wire

Magnetic force between two current carrying wires

$$\mi_{o}\ =\ 4\pi\ \times\ 10^{-7}$$

The Attempt at a Solution

a) the two wires seem to be attracting each other because if they were repulsive, then their angles from the vertical must be the same. According to the right hand rule, the two wires have to point in the same direction in order to have an attractive force with each other.

b&c) I had no idea of how to do them. I just wrote the appropriate equation beneath the letters. This question was the last question from my test in magnetism (by the way I am a grade 12 university student)

If I get the test back, then I will post the solution to this problem, but I would like to see how u people would solve this problem.

 

[doodijh]

by the way the constant was U0

 

[diazona]

Your diagram is so small as to be practically illegible. Could you post a zoomed-in version at higher resolution (and without all that extra space around it)?

 

[doodijh]

Your diagram is so small as to be practically illegible. Could you post a zoomed-in version at higher resolution (and without all that extra space around it)?

ok.
In my new image, imagine the roof as if it was tilted.
& the space around it has nothing to do with the solution of
the problem.

 

[diazona]

The Attempt at a Solution

a) the two wires seem to be attracting each other because if they were repulsive, then their angles from the vertical must be the same. According to the right hand rule, the two wires have to point in the same direction in order to have an attractive force with each other.

Think about this: if they are attracting each other, what's preventing them from coming all the way together and touching?

 

[doodijh]

Think about this: if they are attracting each other, what's preventing them from coming all the way together and touching?

First, it will be absurd to ask in b) of the magnetic force in between them and then set the distance between them as zero (that's what happen when the 2 wires touch each other) If the distance between them is zero, then the equation of the magnetic force will not work.

Second, the angle of theta is bigger than beta, making it obvious that one wire is clearly getting attracted to the other.

Finally, you can not set a picture of two wires attached to each other -> refer back to my first and second reason.

cool

 

[diazona]

First, it will be absurd to ask in b) of the magnetic force in between them and then set the distance between them as zero (that's what happen when the 2 wires touch each other) If the distance between them is zero, then the equation of the magnetic force will not work.

That's true, but the diagram shows you that they are clearly not touching. So that's not a concern.

Second, the angle of theta is bigger than beta, making it obvious that one wire is clearly getting attracted to the other.

Not only is it not obvious, it is wrong. I don't understand how you are coming to that conclusion.

I was asking, if the wires are attracting each other, why is it not the case that $\theta + \beta = 0$? Think about this: if there were no current in these wires and gravity were the only force involved, it would be true that $\theta + \beta = 0$, since both wires would be hanging straight down. Agreed? Now, as the diagram shows, that is clearly not the case. Something is working against gravity. What kind of force between the wires could do that - attractive or repulsive?

 

[doodijh]

That's true, but the diagram shows you that they are clearly not touching. So that's not a concern.


Not only is it not obvious, it is wrong. I don't understand how you are coming to that conclusion.

I was asking, if the wires are attracting each other, why is it not the case that $\theta + \beta = 0$? Think about this: if there were no current in these wires and gravity were the only force involved, it would be true that $\theta + \beta = 0$, since both wires would be hanging straight down. Agreed? Yes

Now, as the diagram shows, that is clearly not the case. Something is working against gravity. What kind of force between the wires could do that - attractive or repulsive?

I think the picture was taken the instant the wires were released, and so u don't know whether the wires will collide or be repellisive to each other. However, you can assume that if one angle is greater than the other then the wire with less angle is the one being attracted, meaning that there is an attractive force between each other. If the two wire were repulsive to each other, then theta and beta will be the same in magnitude.

You thought that the diagram was taken after the wires were released, but I think that the diagram represent an instanteous release of the two wires.

 

[denverdoc]

Why do you assume this? You may be right, but say that the current through one of the loops is much greater than that thru the other. The resultant magnetic field will be much greater in the one case than the other. Now it may the force "felt" by each of the loops will be the same, but I don't see that you have shown that. The other part of this problem that is difficult, is that as the angles change so too will be the magnitude of the cross product, not just because of distance but deviation from right angles of the interacting fields.

Besides, just because the two angles are depicted with different symbols doesn't mean they are different. It may just be a fake out. Altogether a challenging problem for G12.