Solve Optimal Factory Construct Problem for Max Goods in 10-50 Hours

[beamthegreat]

Hi all. I have a rather unique problem that I need help with and I really didn't know how to title it.

Consider the following:

You are trying to build a factory that produces the greatest amount of goods under a given time.

You start off with a construction capacity of 20 per hour and you can choose to construct any of the following structures below in any order.

Structure A: produces 2 goods per hour - Initial cost 5
Structure B: produces 1 goods per hour AND increases the construction capacity by 3 - Initial cost 1
Structure C: produces 1 goods per hour AND increases the construction capacity by 2 - Initial cost 5

There are 2 rules:

1. Each consecutive structure you build increases the cost of the next structure by 1.5x.
2. The amount of goods you produce is calculated precisely at the end of each hour.

______________________________________________

For example, if you choose to construct "A", it will take you 15 minutes (5/20 hours) to complete the first structure. And if you choose to construct an additional "A", it will take you another 22 minutes 30 seconds (5*1.5/20), then 33 minutes 45 seconds (5*1.5²/20) etc, etc.

However, if you choose to construct "B", it will take you 1/20 = 3 minutes to complete the first structure. The next "B" structure would take 3 minute 54.78 seconds (1*1.5 / 20+3), then 5 minutes 11.54 seconds (1*1.5² / 20+[3*2]) etc, etc.As mentioned before, you can alternate between structures so you can switch between any structures freely.Here is a chart of a simulation (probably not optimal) you can take a look to get an idea of how it works:

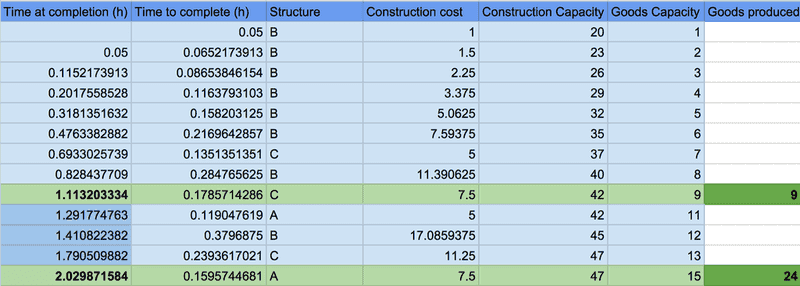
As you can see, building the structures in the following order: B,B,B,B,B,B,C,B,C,A,B,C,A yields a total of 24 goods within 2 hours.

My question is, what is the optimal order to build structures for, 10 hours, 20 hours and 50 hours in order to maximize the amount of goods?

How does one even attempt to solve this problem?

Thanks!

 

[Greg Bernhardt]

Thanks for the post! Sorry you aren't generating responses at the moment. Do you have any further information, come to any new conclusions or is it possible to reword the post?

 

[Stephen Tashi]

I suggest another try at stating the problem. So far, the physical units in the problem are unclear.

You start off with a construction capacity of 20 per hour

That makes "20" sound like a rate of production - 20 goods per hour? 20 structures per hour? Is 20 dollars per hour?

Structure A: produces 2 goods per hour - Initial cost 5

Are "goods" different that "structures"? Does producing structure A produce any goods along with it?

For example, if you choose to construct "A", it will take you 15 minutes (5/20 hours) to complete the first structure.

It would help to have a real world example of when such a calculation makes sense.

 

[beamthegreat]

I suggest another try at stating the problem. So far, the physical units in the problem are unclear.

That makes "20" sound like a rate of production - 20 goods per hour? 20 structures per hour? Is 20 dollars per hour?

"20" is the initial construction capacity of the factory. I chose to omit the unit because I fear it might make the problem more confusing.

For example, you could consider the unit to be square meters, meaning the factory has the capacity to construct one 20 square meter structure per hour.

Are "goods" different that "structures"? Does producing structure A produce any goods along with it?

Yes, structures are different from goods. As I stated, the amount of goods are calculated precisely at the end of each hours. So, constructing structure A will cause it to produce goods at the end of every hour.

Have you looked at my chart? I might be wrong but it should be pretty clear how structures and goods are independent of each other.

Also, to clarify, it does not matter if you complete Structure A at the beginning of the hour or at the very last second before the hour; at the exact end of the hour, you will have 2 goods.

It would help to have a real world example of when such a calculation makes sense.

If you can produce 20 shoes per hour, producing 5 shoes will take you (5/20) of an hour or 15 minutes.

In my case, the factory has the capacity to construct 20 square meters of structures per hour. However, Structure A is only 5 square meters in size, so it will take (5 divided by 20) of an hour to complete the structure.

I apologize for not clarifying this but I assumed this was very basic math.

 

[Mark44]

I can easily understand Stephen Tashi's confusion. Your explanation and table provide very little help in understanding what you are trying to do. It would be much better if you gave an explanation of each column in the table - units involved, what the column means, and definitions of all terms used.

Without knowing what "structures", "goods", "capacity" and other terms mean (terms Stephen Tashi was asking about), the numbers in the table are pretty much meaningless as well as being needlessly precise. For example, one of the construction costs is 17.0859375. Many of the other figures in the table are given to 9 decimal places. They would be just as informative, IMO, rounded to one or two decimal places.

As you can see, building the structures in the following order: B,B,B,B,B,B,C,B,C,A,B,C,A yields a total of 24 goods within 2 hours.

How did you come up with this order?

I apologize for not clarifying this but I assumed this was very basic math.

The math is nothing more complicated than arithmetic, but the rules are very complex and your explanation was very much on the sparse side.

 

[beamthegreat]

How did you come up with this order?

I randomly chose an arbitrary order in order to demonstrate how the process worked.

Without knowing what "structures", "goods", "capacity" and other terms mean (terms Stephen Tashi was asking about), the numbers in the table are pretty much meaningless as well as being needlessly precise. For example, one of the construction costs is 17.0859375. Many of the other figures in the table are given to 9 decimal places. They would be just as informative, IMO, rounded to one or two decimal places.

I'll try to rephrase this question as best I can. If you do not understand anything please tell me how I can better explain it.
Structures are basically objects that improve the performance of the factory. They can accomplish this by either:

1. Improving the construction capacity of the factory (allowing the factory to build structure faster)

2. Increasing the amount of goods that can be produced per hour

3. Any combination of the two points above.

There are three structures you can choose to construct - Structure A, Structure B, and Structure C.

Each of these structure have different sizes and takes different amount of time to construct. The factory can initially build 20 square meters worth of structures per hour. So, if a structure is 5 square meters, it will take (5 divided by 20) hour to complete the structure.

The initial size of each structures are as follow:

Structure A - 5 square meter
Structure B - 1 square meter
Structure C - 5 square meter

However, every subsequent structure of the same type will be 1.5 times larger than the previous structures. For example, structure A's initial size is 5 square meter. After completing the first one, the next one will have to be 7.5 square meter then 11.25, 16.875 etc, etc.

Now the attributes of each structures are listed below:

Structure A: increases the production of goods by 2 per hour
Structure B: increases production by 1 goods per hour AND increases the construction capacity by 3 square meters per hour
Structure C: increases production by 1 goods per hour AND increases the construction capacity by 2 square meters per hour

Once a structure is built, the factory begins constructing another one instantaneously. The order of the structures can be chosen freely without any constraints.

One final important rule is that goods are calculated precisely at the end of each hour.

My question is: in which order should the structures be constructed in order to maximize the goods the factor can produce after 10 hours, 20 hours, and 50 hours.

 

[ellipsis]

Okay, I've studied this problem for the last two days. I've come to two conclusions: The truly optimal solution requires brute-force search, due to the nature of trying to 'pack' the time-sizes into bins of 'hours' - that aspect of the problem is bin-packing. To write a optimal solver, I would encode the possible structure-orders as a trinary number - then it becomes a matter of generating all the trinary numbers up to a certain length, and their associated time-cost and goods-amount.

I think, however, that the greedy algorithm is a very close approximation to the optimal solution - That is, calculate the time-cost for each instance in the sequence, then take the structure which costs the least amount of time. This maximizes the number of structures, and should also nearly maximize the number of goods produced at the end of each hour. This is what I implemented in Excel:

I didn't clean it up at all. I also used minutes instead of hours. This situation is the specs you described, under two hours. It produces 27 goods.

The left 3 columns decide which structure is chosen for building every cycle. As you can see, it follows a certain pattern. Namely,

Build 4 Bs
Loop:
Build 1 C
Build 1 A
Build 1 B
Goto Loop

The math might be basic, but most optimization problems are very difficult. This probably belongs in the computer science board.

 

[Stephen Tashi]

in order to maximize the goods the factor can produce after 10 hours, 20 hours, and 50 hours.

Is the goal to maximize the rate at which the factory can produce goods after those times elapse or is it to maximize the goods actually produced during those times? Once a structure is built,, does it immediately begin producing goods?

 

[beamthegreat]

Is the goal to maximize the rate at which the factory can produce goods after those times elapse or is it to maximize the goods actually produced during those times? Once a structure is built,, does it immediately begin producing goods?

The goal is to maximize the amount of goods produced in within a given timeframe. Once a structure is built, it DOES NOT begin producing goods. It adds to the capacity of the factory and the goods are created at the end of each hour, as stated in the final rule.

 

[Stephen Tashi]

in order to maximize the goods the factor can produce after 10 hours, 20 hours, and 50 hours.

So there are 3 problems to solve? (seeing that the best schedule for 10 hours might not be the best way to start a schedule who goal is to maximize goods produced in 20 or 50 hours)

One thought is to consider what "dynamic programming" says. For example, consider the problem of maximizing the goods produced after 50 hours. if you arrive at hour 49 with G[49] goods , NA[49] machines to type A, NB[49] machines of type B, NC[49} machines of type C, can you find the optimal thing to do in hour 50 as a function of that data? If the structures built during hour 50 will not produce any goods during hour 50, then I suppose it doesn't matter what you you. You could choose not to build any structures. So ask the question for hour 48. The goal is to find the algorithm that makes the decision on what to do in hour n given the data from the previous hour.