- #1
abotiz
- 72
- 0
My assignment is in Swedish so I will try to Translate as good as I can ( if someone knows swedish you can visit the link http://physics.gu.se/~sjogren/FYP100/PM_svaengning.pdf )
We have a swinging Pendulum which equation is given by :
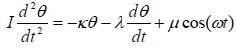
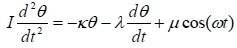
The variables κ, λ and μ are positive constants which are characteristic of the swinging system. θ is the Pendulum angular deviation from the equilibrium position. I = inertia moment
The Question :
Solve the equation in 2 cases
Case 1 : λ=μ=0
Case 2 : λ≠0, μ=0
The Purpose :
Use the Solutions to derive a realtion between the eigenfrequency ω0, damping constant [tex]\gamma[/tex] and angular frequency ωd for the damping Oscillation.
2. The attempt at a solution
Many, and i do not know what to do, because the angular frequency ω = dθ/dt which make the term μ*cos(ω*t) the whole equation into a separable equation ? Iam confused
I need help with this one. A solution to this would be appreciated!
Thanks
Homework Statement
We have a swinging Pendulum which equation is given by :
The variables κ, λ and μ are positive constants which are characteristic of the swinging system. θ is the Pendulum angular deviation from the equilibrium position. I = inertia moment
The Question :
Solve the equation in 2 cases
Case 1 : λ=μ=0
Case 2 : λ≠0, μ=0
The Purpose :
Use the Solutions to derive a realtion between the eigenfrequency ω0, damping constant [tex]\gamma[/tex] and angular frequency ωd for the damping Oscillation.
2. The attempt at a solution
Many, and i do not know what to do, because the angular frequency ω = dθ/dt which make the term μ*cos(ω*t) the whole equation into a separable equation ? Iam confused
I need help with this one. A solution to this would be appreciated!
Thanks