Solve Pulley Mass Q&A: Find Mass of Pulley Given Blocks' Acceleration & Tension

[NotaPhysicsMan]

Alright, here's my Q and A. Please verify

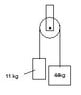
By means of a rope whoe mass is negligible, two blocks are suspended over a pulley, as the drawing shows (attachment). The pulley can be treated as a uniform solid cylindrical disk (I=1/2MR^2) The downard acceleration of the 44.0 kg block is observed to be exactly one-half the acceleration due to gravity. Noting that the tension in the rope is not the same on each side of the pulley, find the mass of the the PULLEY.

Alright, here was my strategy.

Summ of the Torque= (Tension x lever arm )block 1 - (tension x lever arm) block 2)

Sum of torque = moment of inertia x angular acceleration. I=1/2MR^2

Combine two. Tl(block1)- Tl (block 2)= 1/2MR^2 x a

Ok so I don't have Tension 1 or Tension 2. I know the lever arms are basically the radius for each block. I found tension by isolating two situations for the blocks. So for example, block 1:

I know that acceleration (9.81/2) and is positive for B1 and negative for B2.
F=ma or T-W= ma

T=W+ma. I used this to find tension, this tension is equal to the tension on the pulley. so T1 = 162 N, T2=216N.

I have the two T forces.
ok, so plug into equation.
I know that the Radius = lever arm. Also angular acceleration = a/R (sub in.)
TR(block1)- TR (block 2)= 1/2MR^2 x a/R

Ok, I try cancelling the R's.

I get R(T1-T2) = 1/2 MR x a, again the R's cancel.

so 162-216 N =1/2 M x 9.81/2
M= 22kg?


ok, Hopefully I did this right.

 

[CartoonKid]

From my point of view, the net force acting on the pulley is (1/2)(44)(9.81)(R) and the tangential acceleration of the pulley is (1/2)(9.81)=R(alpha). Taking the net force = I(alpha) and do the substituition. Finally I boiled down to m=88kg.

 

[jamesrc]

Looks good to me.

When you say: "I know the lever arms are basically the radius for each block.", I think you mean that you know that the lever arms are exactly the radius of the pulley. (We're not worrying about rope thickness, mass, or extensibility here.)

Was there anything in particular that you weren't comfortable with?

 

[NotaPhysicsMan]

Huh? I have no clue what you did? where's the 11 kg come in?

 

[NotaPhysicsMan]

Cartoon kid, got 88 kg, was confused with his way of doing it that's all.

 

[Gokul43201]

Nota...you've got it right. I get 22kg too.

Not sure where Cartoon got that expression for net force (by which, I think he means 'net torque')

 

[NotaPhysicsMan]

Ok Great. You guys must be profs outside of this forum? These problems takes me at least 30min to about 1 hr or more sometimes. That's why I get screwed for exams lol.

Now, for my second part lol:

A small 0.500 kg object moves on a frictionless horizontal table in a circular path of radus 1.00m. The angular speed is 6.28 rad/s. The object is attached to a string of negligible mass that passes through a small hole in the table at the center of the circle. Someone under the table begins to pull the string downard to make the circle smaller. If the string will tolerate a tension of no more than 105 N, what is the radius of the samllest possible circle on which the object can move?

Ok my work:

I know that since it's frictionless, the momentum must be conserved.

So L final = L initial.

Iw final = Iw initial
or
(mr^2)w (final)= (mr^2)w (initial)
I have the initial values for m, r, and w. And only the m value for the final values. So I need ultimately r, and on the side, w.

Masses cancel out.
I can substitute w for v/r?

well I did and I get.

(r^2)v/r (final)=(r^2)v/r (initial) Cancel out the possible r's

rv final = rv initial.

Ok I have tension as 105 N. F=ma
T=ma a=v^2/r
T=m(v^2/r)

ok so plug in numbers and solve for V. V final = 14.49m/s.

ok now sub all values into rv final = rv initial and solve for r final.
V initial can be converted by multiplying the w=6.28 rad/s by radius of 1.00m

I get 0.435 m for r final. It makes some sense, as the value is smaller.

 

[CartoonKid]

Sorry for the wrong solution. I know why I got it wrong already.

 

[CartoonKid]

Your working for second part is correct up to this point:
Ok I have tension as 105 N. F=ma
T=ma a=v^2/r
T=m(v^2/r)
You are taking r=1m which is the initial radius. This is not correct.

 

[jamesrc]

NotaPhysicsMan:

You may be running into trouble because you're notation is not clean:

1. Angular Momentum is Conserved (you're good here until you write your equation; remember that the initial radius is different from the final radius):

L_i = L_f
mr_i^2\omega_i = mr_f^2\omega_f
Solve for ω_f:
\omega_f = \left(\frac{r_i}{r_f}\right)^2\omega_i

Now find the tension in the rope (no need to consider the tangential velocity, just balance the tension with the centripetal force):

\Sigma_r F = mr\omega^2 = T

at the point of breaking, the tension is equal to its maximum value:

mr_f\omega_f = T_{\rm max}

Solve for r_f in terms of known quantities by substituting in your expression for ω_f:

mr_f\left(\left(\frac{r_i}{r_f}\right)^2\omega_i\right) = T_{\rm max}

(...algebra...)

r_f = \left(\frac{m\omega_i^2r_i^4} {T_{\rm max}}\right)^{\frac 1 3}

I get a different answer than you do when I plug in the numbers. You can check your work by using your calculated r to find ω, then check the tension in the cable to see if it is 105 N.

 

[Doc Al]

I get 0.435 m for r final. It makes some sense, as the value is smaller.

Try doing the problem more directly, keeping things in terms of angular speed rather than converting to linear speed (less chance of error):
\omega R^2 = \omega_1 R_1^2
T = m \omega^2 R

Solve these two equations for R; \omega_1, R_1, and T are given.

 

[NotaPhysicsMan]

T = m \omega^2 R: Here's a question, you guys have that for equating centripetal force equation and tension. Isn't centripetal force suppose to indirectly proportional to the R? Formula sheet says Fc=(mv^2)/R or T=(mw^2)/R. Either way, thanks for the help.

 

[jamesrc]

Your formula sheet has a typo. Say v = Rω

start with:

F_c = \frac{mv^2}{R}

substitute in for v:

F_c = \frac{m\left(R\omega\right)^2}{R}

Simplify:

F_c = mR\omega^2

 

[NotaPhysicsMan]

Ahh, I see how that works. Thanks again. Wasn't a typo, just my bad lol.