Puzzles
- 21
- 0
Hey everyone, it's me again with yet another recurrence equation I've been stuck with:
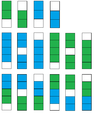
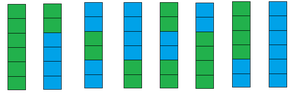
Using recurrence relations (recurrence equations... is it the same thing?), solve the following: There is a chart with dimensions 1xn. We have dominoes in two different colors which we should use to fill up the chart. In how many different ways can the chart be filled?
The way I understand it, a single domino will take up two spaces. Therefore, we have n/2 places to put the dominoes in, and 2 choices at each place. However, I'm not certain about the whole "a single domino will take up two spaces" if it's a correct assumption at all - I'm afraid I don't understand the problem well enough. In any case, if this is the solution, it has nothing to do with recurrence relations, and I have no idea how to even start with those.
Very obviously, I'm hopeless with recurrence problems. I hope someone can explain how this particular problem should be solved using recurrence relations. Thank you :)
Using recurrence relations (recurrence equations... is it the same thing?), solve the following: There is a chart with dimensions 1xn. We have dominoes in two different colors which we should use to fill up the chart. In how many different ways can the chart be filled?
The way I understand it, a single domino will take up two spaces. Therefore, we have n/2 places to put the dominoes in, and 2 choices at each place. However, I'm not certain about the whole "a single domino will take up two spaces" if it's a correct assumption at all - I'm afraid I don't understand the problem well enough. In any case, if this is the solution, it has nothing to do with recurrence relations, and I have no idea how to even start with those.
Very obviously, I'm hopeless with recurrence problems. I hope someone can explain how this particular problem should be solved using recurrence relations. Thank you :)