- #1
yuri6996
- 2
- 0
can anyone advise me any way to convert this equation to s-domain by using laplace transform
TQ...
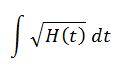
TQ...
Last edited: