- #1
Wilmer
- 307
- 0
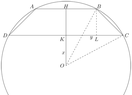
A circle radius = 725 contains 4 isosceles
trapezoids, length of shorter parallel sides = 666.
Heights, other parallel sides, and equal sides are all integers.
What are the 4 heights?
trapezoids, length of shorter parallel sides = 666.
Heights, other parallel sides, and equal sides are all integers.
What are the 4 heights?