Solve the homogenous Neumann problem

[chwala]

TL;DR Summary

See attached

I am going through this notes and i would like some clarity on the highlighted part...the earlier steps are pretty easy to follow...

Is there a mistake here...did the author mean taking partial derivative with respect to $t$? is $\dfrac{d}{dt}$ a mistake? How did that change to next line $\dfrac{∂}{∂t}$... unless i am the one missing something here. Cheers guys.

 

[jedishrfu]

Its just a notation convention, taking the partial is the same as taking a derivative.

As you move the derivative operation inside the integral, you realize that you now have more than one variable and so switch to the partial derivative notation and that you are not taking the derivative of x ie x is independent of t.

 

[chwala]

Its just a notation convention, taking the partial is the same as taking a derivative.

As you move the derivative operation inside the integral, you realize that you now have more than one variable and so switch to the partial derivative notation and that you are not taking the derivative of x ie x is independent of t.

Thanks for that...considering it as a 'notation convention' makes sense. I was lingering there for some time trying to figure out on what's happening man... thanks @jedishrfu. Bingo!

 

[pasmith]

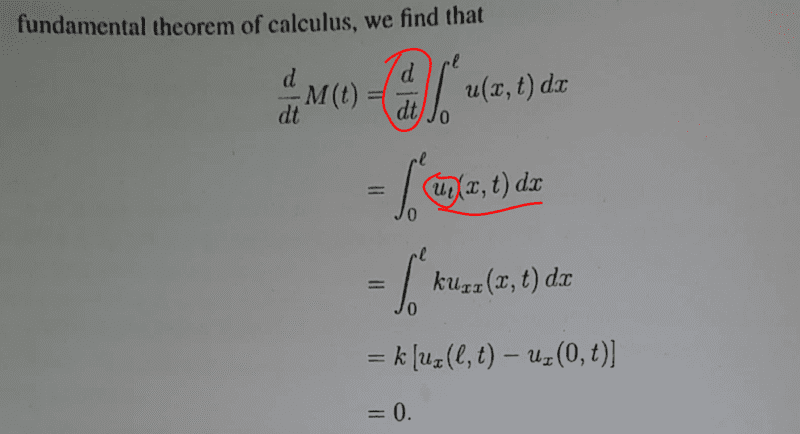
Is there a mistake here...did the author mean taking partial derivative with respect to $t$? is $\dfrac{d}{dt}$ a mistake? How did that change to next line $\dfrac{∂}{∂t}$... unless i am the one missing something here. Cheers guys.

$\int_0^l u(x,t)\,dx$ is a function only of $t$, in the same way that $\int_a^b f(x)\,dx$ is just a number: the result of a definite integration is not a function of the dummy variable. So the total derivative is correct. When we swap the order of integation with respect to $x$ and differentiation with respect to $t$ we have by the definitions of total and partial differentiation that $$\begin{split} \frac{d}{dt}\int_0^l u(x,t)\,dt &= \lim_{h \to 0} \frac{1}{h}\left(\int_0^l u(x,t+h)\,dx - \int_0^l u(x,t)\,dx\right) \\ &= \int_0^l \lim_{h \to 0} \frac{u(x,t+h) - u(x,t)}{h}\,dx \\ &= \int_0^l u_t(x,t)\,dt.\end{split}$$