chwala
Gold Member
- 2,827
- 415
- Homework Statement
- see attached
- Relevant Equations
- numerical analysis
I need insight on ##Q.2 (ii)## part only,

find mark scheme here;
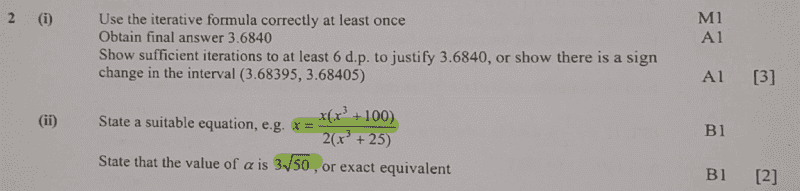
How do we determine suitable equation, ##x=x...##?
ok, just looking at the solution, we shall have;
##2x^3+50 = x^3+100##
##x^3=50##
→##x##=##\sqrt[3]50##≡##3.68403## which is the value of ##α## ( convergent value as indicated in previous step).
I think it was an error to indicate ##3\sqrt 50## ...am assuming it was a typo error which is a bit misleading...been cracking my head trying to figure out on this.
find mark scheme here;
How do we determine suitable equation, ##x=x...##?
ok, just looking at the solution, we shall have;
##2x^3+50 = x^3+100##
##x^3=50##
→##x##=##\sqrt[3]50##≡##3.68403## which is the value of ##α## ( convergent value as indicated in previous step).
I think it was an error to indicate ##3\sqrt 50## ...am assuming it was a typo error which is a bit misleading...been cracking my head trying to figure out on this.
Last edited: