chwala
Gold Member
- 2,827
- 415
- Homework Statement
- See attached
- Relevant Equations
- understanding of probability distribution concept...
This is the problem;

Find my working to solution below;

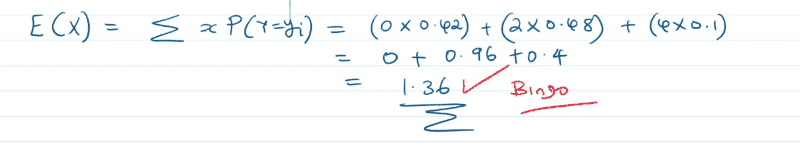 find mark scheme solution below;
find mark scheme solution below;

I seek any other approach ( shorter way of doing it) will be appreciated...
Find my working to solution below;
I seek any other approach ( shorter way of doing it) will be appreciated...