Solve the problem involving linear programming

[chwala]

Homework Statement

see attached

Relevant Equations

linear programming

Find question and solution here;

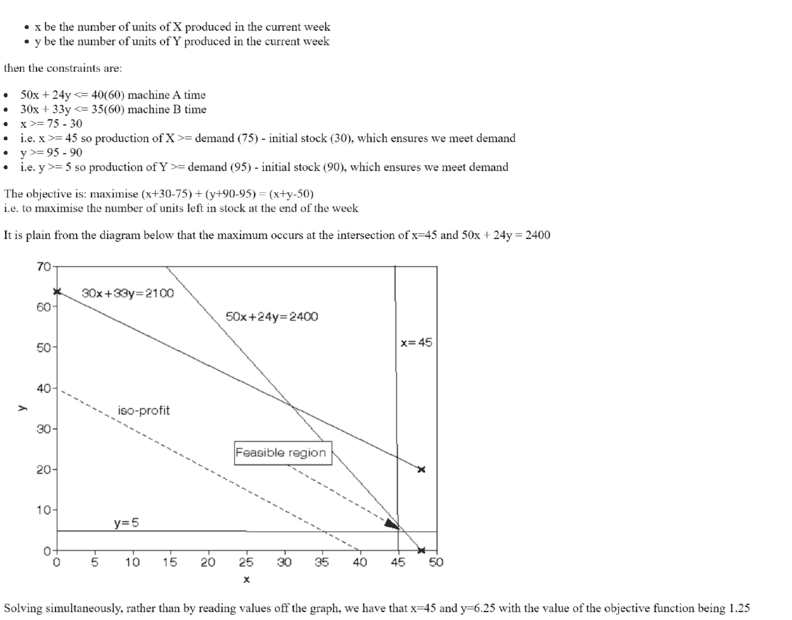
The initial steps were a bit confusing to me...i decided to use hours instead of minutes ...only then did it become more clear to me. See my graph,

Ok i follow that the function would be optimised at $x=45$ and $y=6.25$ ...now to my question...we cannot have $y=6.25$ products...a product can only take natural numbers, $1,2,3...$
I can follow that the objective function would be $=1.25$ this is clear...only on the part of $y=6.25$.

 

[Steve4Physics]

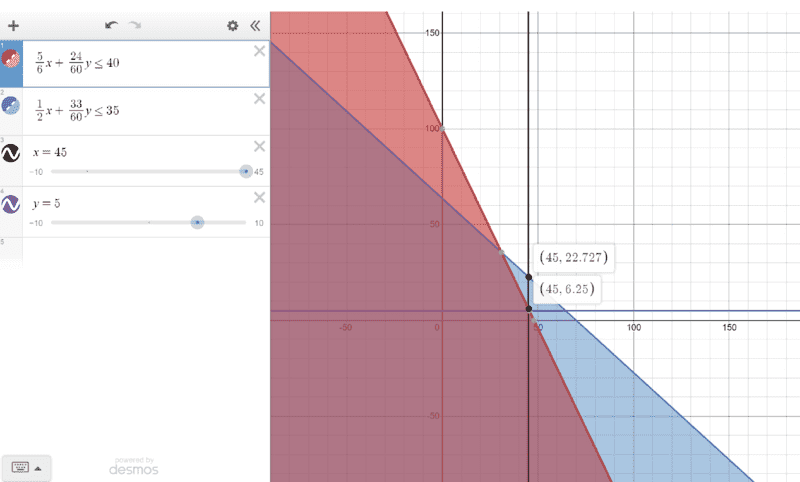
Ok i follow that the function would be optimised at $x=45$ and $y=6.25$ ...now to my question...we cannot have $y=6.25$ products...a product can only take natural numbers, $1,2,3...$
I can follow that the objective function would be $=1.25$ this is clear...only on the part of $y=6.25$.

There is no reason to expect integer-value answers

For example, exactly the same equations would apply if A and B were types of liquid with x and y representing the number of litres produced of each.

There is no reason why the optimal solution should give exact numbers of litres. In fact you would generally expect non-integer answers.

In your problem, as a final step, you might want to round-down to the nearest integer giving y=6 and the objective function = 1.

 

[chwala]

True I had fixated my thinking solely on solid products...its true that the products could be of liquid or gaseous form... implying that the solution given is correct.