Solve the simultaneous congruence modulo equation

[chwala]

Homework Statement

See attached

Relevant Equations

pure maths/ Extended euclidean algorithm

Find question and solution here;

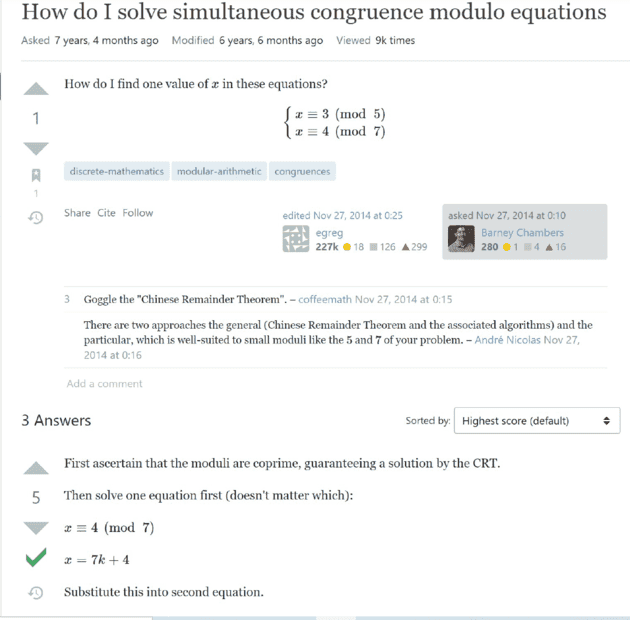
The steps are clear...out of interest i decided to use the other equation; may i say that i underestimated the euclidean algorithm ...in trying to find the inverse of modulo arithmetic...of course we have the online calculator..but i always like understanding (indepth )on any math concept...some deep thinking on reverse substitution...My approach is as follows;

$x≡3 (mod5)$
$x= 5k+3$
$5k+3≡4(mod7)$
$k=(1)(5^{-1})(mod 7)$
now on using Extended Euclidean algorithm, it follows that,
$1=5-(7-5(1))(2)$
$1=5-(14-5(2))$
$1=5(3)-(7)(2)$
Therefore the inverse of $5=3$, then we shall have
$k=(1)(3)(mod 7)$
$k=7n+3$
$x=5(7n+3)+3$
$x=35n+18$...any other easier approach highly appreciated.

 

[anuttarasammyak]

Let x = y(mod 35),
y<35
y=3 (mod 5)={3,8,13,18,23,28,33}
y=4(mod 7)={4,11,18,25,32}
So y=18.

 

[chwala]

Let x = y(mod 35),
y<35
y=3 (mod 5)={3,8,13,18,23,28,33}
y=4(mod 7)={4,11,18,25,32}
So y=18.

correct ,yes but wondering if your working steps is acceptable. Cheers mate. ...you looked at a common 'remainder' to conclude on $18$.

 

[nuuskur]

Not clear what you mean by "easier". Chinese remainder theorem (CRT) is as easy as it gets if the moduli are pairwise coprime. For more in depth analysis, study a proof for the CRT.

Also, would recommend not posting screenshots of other websites. Link it, instead.