chwala
Gold Member
- 2,827
- 415
- Homework Statement
- see attached
- Relevant Equations
- Vertical stretch/compression knowledge
This is the problem,
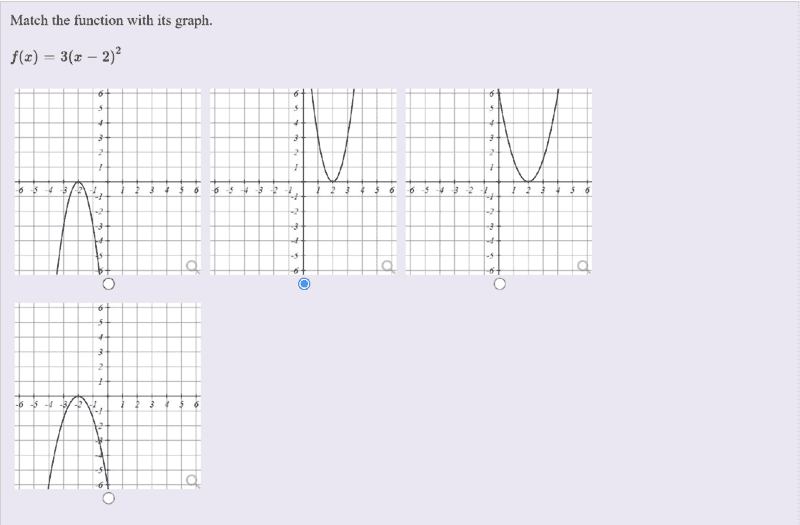
Let ##y=f(x)= (x-2)^2##. The graph of ##y=af(x)##can be obtained from the graph of ##y=f(x)## by a stretch parallel to the y- axis with scale factor ##a##. In our case here, ##a=3##, therefore the corresponding graph is as indicated in blue. Find my graph below using desmos.
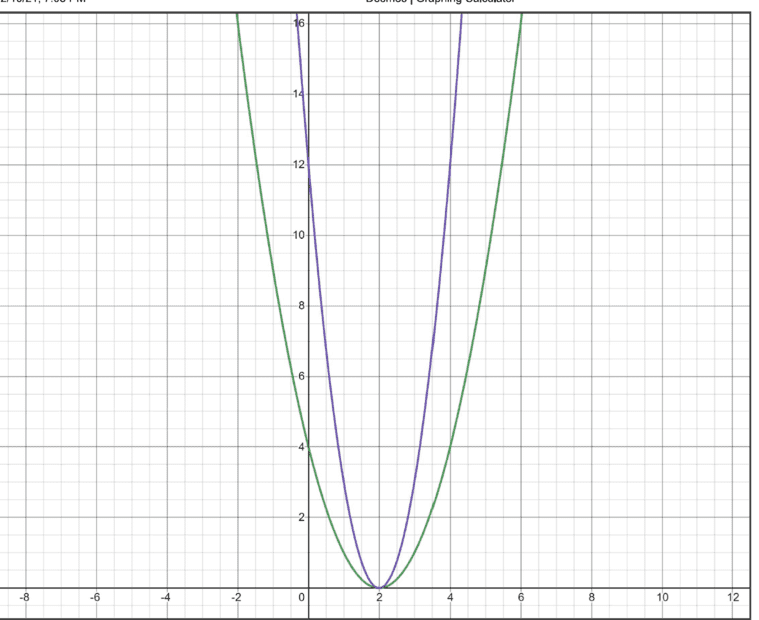
Let ##y=f(x)= (x-2)^2##. The graph of ##y=af(x)##can be obtained from the graph of ##y=f(x)## by a stretch parallel to the y- axis with scale factor ##a##. In our case here, ##a=3##, therefore the corresponding graph is as indicated in blue. Find my graph below using desmos.
Last edited: