Solve Work Energy Problem: Calculate Velocity v at B

[Warr]

I'm confused about this problem. (a diagram is included below)..

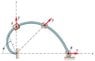
The 0.5 kg collar slides with negligible friction along the fixed spiral rod, which lies in the vertical plane. The rod has the shape of the spiral r = 0.3$$\theta$$, where r is in meters and $$\theta$$ is in radians. The collar is released from rest at A and slides to B under the action of a constant radial force T = 10 N. Calculate the velocity v of the slider as it reaches B.

Could someone help me get this started

I think it could be written $${{\int_{\frac{\pi}{2}}}^{\pi}T\cdot(0.3)d\theta= \frac{1}{2}mv_f^2$$

..is this even valid. If its not, then if I just wrote $$T\cdot{dr}$$, then how do I find T in terms of r, or find the relationship between T and the direction of dr.

Thanks for any input.

 

[mezarashi]

Your approach was on the right track in my opinion. However, I don't know if it is safe to not put gravitational potential into the picture as well. In anycase, the first step is to figure out how much work was done on the collar.

In circular coordinates, the work is equal to the Torque dot product with the change in angle. The torque vector can be expressed as a magnitude multiplied by a unit vector. In this case it has a magnitude of ten and a direction along r. You can immediately express r as a function of the change in angle, thus go ahead and integrate... now if I can only figure out how to work LaTeX...

 

[Physics Monkey]

Warr,

You don't need to worry about the gravitational potential energy because the particle doesn't make any net change in its height. Your approach using the work energy theorem should work. In order to calculate the work done by the radial force, you need to figure out its component along the direction of motion. This component changes as the particle moves on the spiral track and you need to know how it changes.

 

[Warr]

Ok, now I'm confused. After reading mezarashi's post, I realized I had forgotten gravitation potential. But now you say I don't need it because there is no change in net height..but it starts at $$h_o=\frac{0.3\pi}{2}$$ and ends at [/tex]h_f=0[/tex]..so doesn't it make a net change, and therefore the equation would be $${{\int_{\frac{\pi}{2}}}^{\pi}T\cdot(0.3)d\theta - mg\Delta{h}= \frac{1}{2}mv_f^2$$

which would give me $$v_f=5.3\frac{m}{s}$$

is this right?

 

[Physics Monkey]

Warr,

My apologies, I assumed the bead was starting at $$\theta = 0$$ and didn't see your lower limit of integration there. Also, even though it now makes a change in height, the work energy theorem in the form
$$K_f - K_i = W$$ is still valid, but if you use this form you must include the work done by gravity. It will be simpler to equate the total change in energy (kinetic plus potential) to the work done by the external force.

Edit:
Your formula for the work done by T seems ok, I made a slight mistake in my own calculation. It is however important that you use $$\vec{F}\cdot d\vec{r}$$ in general. It happens to reduce to your formula in the present case.

 

[Physics Monkey]

Also, I would point out that you can find a potential to go with the external force T as well. This makes the problem super easy because then you can use conservation of energy.

 

[mezarashi]

Taking a good look at your problem, I find that it is a bit more complex than I first thought. I hope latex works this time -.-

Ignore gravity for now. It's easy to add it later once we find the work done on the collar by the force T. The main equation is still:

$$\int \tau d\theta \mbox{ where }&\tau=\vecT\times\vecr$$
(note: alright, I'm giving up with latex soon...-_-)
OMG! I've been at it for 10 minutes. I give up. I hate LATEX!

Work = Integral( torque dtheta)
where torque = T x r

Alright, here we have the hard part. How do we find the cross product of the force vector T and the position vector r.

You should try to take a infinitely small portion of the curve and analyze it. Now this needs some drawings. Let me paintshop a bit first. Get back to you later.

 

[mezarashi]

Um, here. Although I'm not 100 positive whether my estimatations are correct, but seems logical enough. Unless you have the answer, then I would have something to work towards :p

I guess you can't attach pictures here. Only links.
http://images5.theimagehosting.com/4322ff.GIF"