Solving a Disk Method Problem: What Info Needed?

[JProgrammer]

So I am trying to find the volume of a solid with this information given to me:

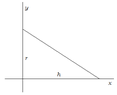
𝑥=0
𝑦=0
𝑦=−2𝑥+2

However, when I go to enter this information into a disk method calculator, I don't have enough information to enter into the calculator, such as the lower function and limits.

My question is: what information would I use to find the volume using the disk method?

Thank you.

 

[MarkFL]

What is the axis of rotation?

 

[MarkFL]

Let's consider the line given by:

$$\frac{x}{h}+\frac{y}{r}=1$$ where $$0<h,r$$

Observing that this is the two-intercept form of a line, we should recognize that the graph of the line (in the first quadrant) will be as follows:

View attachment 5987

Now, if we take the $x$-axis as the axis of rotation, we should see that the solid of revolution will be a cone of radius $r$ and height $h$, and thus the volume $V$ of the solid of revolution will be (using the formula for the volume of a cone):

$$V=\frac{1}{3}\pi r^2h$$

So, we know what our goal is. Now, if we are going to use the disk method, then we can look at an element of the volume, which is naturally, a disk (actually a cylinder with height $H=dx$):

$$dV=\pi R^2H$$

Now, as mentioned, we have $H=dx$ and we observe that $R=y$, but we want $R$ in terms of $x$, hence we solve the equation of the line for $y$ to get $y$ as a function of $x$:

$$y=\frac{r}{h}(h-x)$$

And so we may now state:

$$dV=\pi\left(\frac{r}{h}(h-x)\right)^2\,dx=\frac{\pi r^2}{h^2}(x-h)^2\,dx$$

Hence:

$$V=\frac{\pi r^2}{h^2}\int_0^h(x-h)^2\,dx$$

Let:

$$u=x-h\implies du=dx$$

And we have:

$$V=\frac{\pi r^2}{h^2}\int_{-h}^0 u^2\,du=\frac{\pi r^2}{h^2}\cdot\frac{h^3}{3}=\frac{1}{3}\pi r^2h$$

 

[MarkFL]

Now, suppose we wish to check our work using the shell method...

$$2V=2\pi RH\,dy=2\pi yx\,dy=2\pi y\cdot\frac{h}{r}(r-y)\,dy=\frac{2\pi h}{r}y(r-y)\,dy$$

Hence:

$$V=\frac{2\pi h}{r}\int_0^r y(r-y)\,dy=\frac{2\pi h}{r}\left[\frac{r}{2}y^2-\frac{1}{3}y^3\right]_0^r=\frac{\pi h}{3r}\left[3ry^2-2y^3\right]_0^r=\frac{\pi h}{3r}\left(3r^3-2r^3\right)=\frac{1}{3}\pi r^2h\quad\checkmark$$