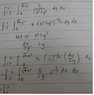- #1
chetzread
- 801
- 1
Homework Statement
in this problem , i couldn't express all the x any y in terms of u( refer to the circled part ) ... so , i have problem to proceed my subsequent steps ...
Homework Equations
The Attempt at a Solution
i let u = (x^2) + (y^2) ... [/B]