- #1
Saptarshi Sarkar
- 99
- 13
- Homework Statement
- Consider the situation demonstrated in the image below. A man standing a distance L away from the cliff throws a ball with speed v at an angle ϕ with the vertical. Height of the cliff is H and its slope makes an angle θ with the horizontal.
After laying down a suitable coordinate system
(a) Find the equation of the trajectory of the ball.
(b) Find the equation of the slope of the hill.
(c) Non-dimensionalize both the equations. How many free parameters are left in the problem?
(d) Construct a Manipulate command by varying all the free parameters in a suitable range. Play with parameters to find out in what cases you have ball land somewhere on the slope. What is the condition for which ball will hit the edge of the cliff (top of the cliff).
(e) Validate your observations in part (d) by doing algebraic calculations.
- Relevant Equations
- ##y_{ball}=ax^2+bx+c##
##y_{cliff}=dx+e##
The question is

I have tried solving this problem several times over several days but each time the plot I get gets weird. Can someone please check what I did wrong?
My attempt is attached below (I did not non-dimensionalize it as I wanted to first check if my code works)

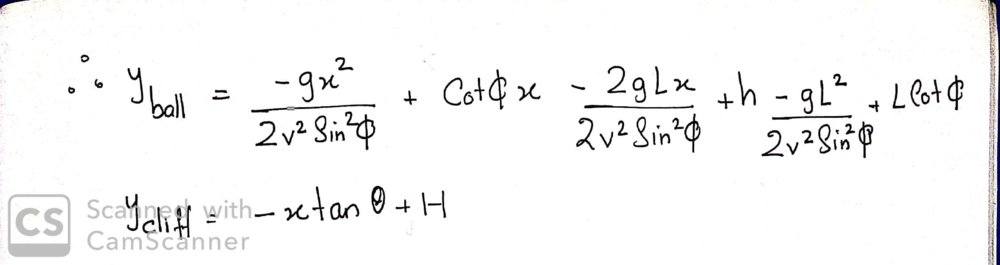
The Mathematica code I wrote is
Manipulate[Plot[{((-9.8 x^2)/(2 (v Sin [\[CapitalPhi]])^2)) + Cot[\[CapitalPhi]] x - ((9.8 L*x)/(v Sin [\[CapitalPhi]])^2) + h - ((9.8 L)^2)/(2 (v Sin [\[CapitalPhi]])^2) + L Cot[\[CapitalPhi]], -x Tan[\[CapitalTheta]] + H}, {x, -10, 10}, PlotRange -> {0, 20}], {v, 1, 10}, {\[CapitalPhi], 0.001, Pi/2}, {L,0, 10}, {h, 0, 10}, {H, 0, 10}, {\[CapitalTheta], 0, Pi/2}]
Please Help!
You can get the lecture notes here, which contains a similar solved example on page 5.
I have tried solving this problem several times over several days but each time the plot I get gets weird. Can someone please check what I did wrong?
My attempt is attached below (I did not non-dimensionalize it as I wanted to first check if my code works)
The Mathematica code I wrote is
Manipulate[Plot[{((-9.8 x^2)/(2 (v Sin [\[CapitalPhi]])^2)) + Cot[\[CapitalPhi]] x - ((9.8 L*x)/(v Sin [\[CapitalPhi]])^2) + h - ((9.8 L)^2)/(2 (v Sin [\[CapitalPhi]])^2) + L Cot[\[CapitalPhi]], -x Tan[\[CapitalTheta]] + H}, {x, -10, 10}, PlotRange -> {0, 20}], {v, 1, 10}, {\[CapitalPhi], 0.001, Pi/2}, {L,0, 10}, {h, 0, 10}, {H, 0, 10}, {\[CapitalTheta], 0, Pi/2}]
Please Help!
You can get the lecture notes here, which contains a similar solved example on page 5.