greg_rack
Gold Member
- 361
- 79
- Homework Statement
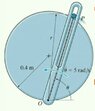
- The smooth particle P is attached to an elastic cord extending from O to P. Due to the slotted arm guide, P moves along an horizontal path(##r=0.8sin(\theta)##) with constant angular velocity of ##\dot{\theta}=5rad/s##.
The mass of P is 0.08kg, the cord stiffness is k=30N/m and its unstretched length 0.25m.
Find the forces of the guide acting on P for theta=60
- Relevant Equations
- velocity and acceleration components in polar coordinates, Newton's 2nd law.
Hello guys,
here's a problem which I'm having troubles solving.
It asks for the forces acting on P when ##\theta=60^{\circ}##.
I thought for this problem it would have been convenient to consider a polar reference system(r, theta). Drawing the FBD of pin P at a moment in time, we will have 3(?) forces acting on P:
-one(##F_S##) along the r direction(pointing towards O caused by the spring-modeled cord, function of its stretch and k;
-one(##F_P##) along the positive(direction of movement) theta direction, caused by the push "from backwards" of the guide exerted on P;
-a last normal force, exerted by the circle normal to the path, thus not aligned with the r-theta system defined.
Could you tell me if these are all the forces acting, and thus the equations of motion(FBD+KD) might be built from them?
In case yes, now we could start writing down the EOMs to solve for ##F_P##.
$$
\left\{\begin{matrix}
F_S-Ncos\phi=m(\ddot{r}-r\dot{\theta}^2)\\
F_P-Nsin\phi=m(r\ddot{\theta}+2\dot{r}\dot{\theta})
\end{matrix}\right.$$
We may calculate ##F_S## from Hooke's law, but to solve for ##F_P## and N we still need ##\phi##.
The procedure to calculate such angle seemed kinda convoluted and thus got me thinking I wasn't on the right path... I was as well confused on the problem's request: do they mean "my" ##F_P## by "forces of the guide acting on P"?
Greg