Darkmisc
- 222
- 31
- Homework Statement
- Is there a mistake in the below solution?
- Relevant Equations
- Definite integrals
Hi everyone
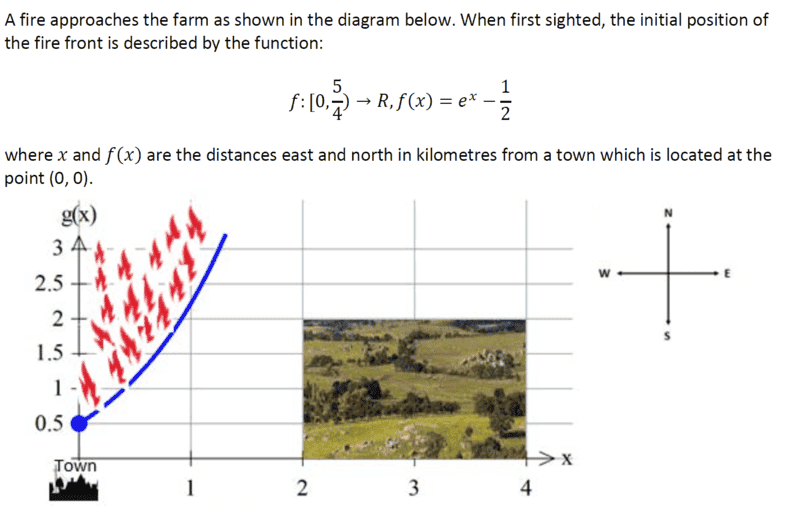
To solve the below problem, I assumed the affected area was 2x2 minus the definite integral of the given function between 2 and 4.
I then equated the answer for that with the given function to solve for a, b and c.
I don't know why the solutions give b as 2ln5.
Have I made a mistake, or are the solutions wrong?
Thanks
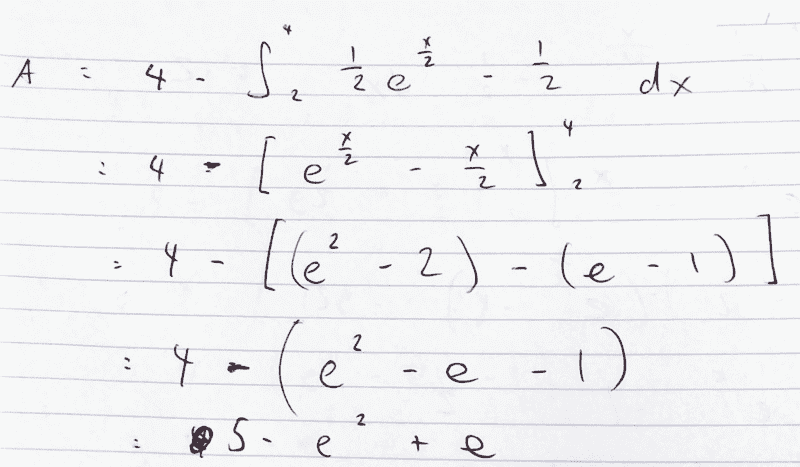
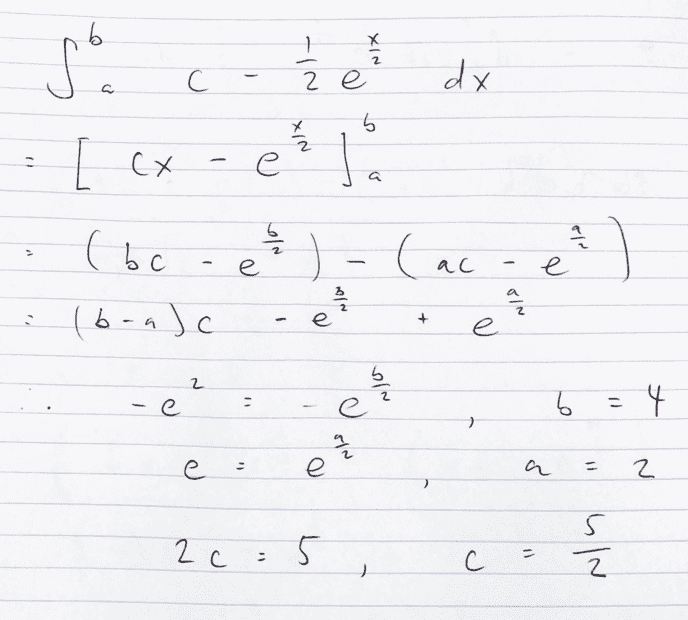


To solve the below problem, I assumed the affected area was 2x2 minus the definite integral of the given function between 2 and 4.
I then equated the answer for that with the given function to solve for a, b and c.
I don't know why the solutions give b as 2ln5.
Have I made a mistake, or are the solutions wrong?
Thanks
Attachments
Last edited by a moderator:
