- #1
Bewilder
- 2
- 0
I am trying to find the steady states in the ODE system. Assuming y0 = 2.5 * 10^5, I want to calculate y1, y2, y3 at the steady state. I do not understand how this would be possible, because only y0 is given and the following:
d0 = 0.003,
d1 = 0.008,
d2 = 0.05,
d3 = 1,
ry = 0.008,
ay = 1.6/100,
by = 10/750,
cy = 100,
u = 4 * 10^−8,
y0 = 2.5 * 10^5.
This is my ODE system:
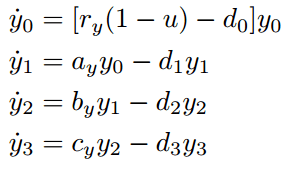
My task says: Find algebraically the steady state for the equations. Set y0 = 2.5 * 10^5 and calculate y1, y2, y3 based on the derived equations at the steady state.
Is it even possible to find the exact value of y1, y2, and y3 with the given information?
I have tried it in R, but it's impossible to get an answer.. How can I do this manually to get the solution for y1, y2, y3 at the steady state?
d0 = 0.003,
d1 = 0.008,
d2 = 0.05,
d3 = 1,
ry = 0.008,
ay = 1.6/100,
by = 10/750,
cy = 100,
u = 4 * 10^−8,
y0 = 2.5 * 10^5.
This is my ODE system:
My task says: Find algebraically the steady state for the equations. Set y0 = 2.5 * 10^5 and calculate y1, y2, y3 based on the derived equations at the steady state.
Is it even possible to find the exact value of y1, y2, and y3 with the given information?
I have tried it in R, but it's impossible to get an answer.. How can I do this manually to get the solution for y1, y2, y3 at the steady state?
Code:
model <- function(t,x,params){
y0 <- x[1]
y1 <- x[2]
y2 <- x[3]
y3 <- x[4]
ry <- params[1]
mu <- params[2]
d0 <- params[3]
ay <- params[4]
d1 <- params[5]
by <- params[6]
d2 <- params[7]
cy <- params[8]
d3 <- params[9] m <- rep(0,4)
m[1] = ((ry*(1-mu)) - d0) * y0
m[2] = (ay * y0) - (d1 * y1)
m[3] = (by * y1) - (d2 * y2)
m[4] = (cy * y2) - (d3 * y3)
return(m)
}
x <- ode23(model, y0 = c(y0=250000, y1=y_1, y2=y_2, y3=y_3), t0=0,tf=400, params = c(0.008,4*10^-8,0.003,1.6/100,0.008,10/750,0.05,100,1))