Solving AC Circuits: Vin, R, L & C Values

[Mutaja]

Homework Statement

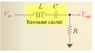
The AC circuit is the following:

V_in = 10√2*sinωt V
R = 5 Ω
L = 5 mH
C = 100 µF

a) what is V_out when the frequency (f) is 100hZ

Homework Equations

The Attempt at a Solution

After two weeks of spring break in addition to Easter holiday, I'm well and truly out of shape when it comes to 'homework'.

I need to solve this, simply because it's relevant to what I study. My book covers just about anything, but I can't seem to find examples on how to solve this - it might be because I'm not sure what I'm looking for.

I'm looking to find the V_out. The problem with this is my understanding of how voltage works. Voltage is something that's across a component, and in that case, V_out will be equal to V_R in my circuit above, right?

I also can't find any formulas in my book that covers this topic. I'm fully aware that's because I can't find it - I know it's there. I would just like some guidance as to where I can start solving this. I will continue looking through my book in addition to using google.

Thanks for any input, and I apologize for this vague question - I just need to get started after spending too long off the subject.

 

[gneill]

The "LC" leg and the R form a voltage divider. So:

Look up the formulas for the impedances of reactive components (inductors, capacitors).
Look up the formula for a voltage divider.

 

[Mutaja]

The "LC" leg and the R form a voltage divider. So:

Look up the formulas for the impedances of reactive components (inductors, capacitors).
Look up the formula for a voltage divider.

Alright.

Impedance for inductors: X_L = ωL

Impedance for capacitors: X_C = $\frac{1}{ωC}$

Voltage divider rule for AC circuits: V_ZX= $\frac{ZX}{ZT}$ * V_T

Z_X being the impedance of the component I'm calculating the voltage drop across.

Z_T is the total impedance of the circuit.

V_T would be supplied voltage, in this case, V_IN

So here's my attempt:

Z_T = X_C + X_L + R
Z_T = $\frac{1}{ωC}$ + ωL + R
Z_T = $\frac{1}{2∏*100Hz*100μC}$ + 2∏*100Hz*5mH + 5Ω
Z_T = 15.91Ω + 3.14Ω + 5Ω
Z_T = 24.05 Ω

Z_X = 15.91Ω + 3.14Ω
Z_X = 19.05Ω

V_OUT = $\frac{ZX}{ZT}$ * V_IN
V_OUT = $\frac{24.05Ω}{19.05Ω}$ * 10*√2*sinωtV
V_OUT = 1.26 * 10*√2*sinωtV

Things are starting to make sense again, and I got to say, I really enjoy doing this. Progress is king.

Assuming some of the above work is correct, I have a couple of questions. t is the time constant of the sinus wave. When t is 0, the voltage is 0. Should my answer then be V_OUT(t) = 17.82sinωtV ?

Also, isn't AC voltage/current given in complex numbers? Sorry for the stupid questions. Hopefully I'll get back into this soon enough :)

Really appreciate your help, gneill.

 

[gneill]

Alright.

Impedance for inductors: X_L = ωL

Impedance for capacitors: X_C = $\frac{1}{ωC}$

Those are reactances, the magnitude of the impedances which are complex values. So what you want are:

Impedance for inductors: X_L = jωL

Impedance for capacitors: X_C = $\frac{1}{jωC}$


Complex values are used because they represent phasor values, and phasors are what you want to work with for AC circuits. Let's you determine not only the magnitudes of currents and voltages but their relative phases, too.

Voltage divider rule for AC circuits: V_ZX= $\frac{ZX}{ZT}$ * V_T

Z_X being the impedance of the component I'm calculating the voltage drop across.

Z_T is the total impedance of the circuit.

V_T would be supplied voltage, in this case, V_IN

So here's my attempt:

Z_T = X_C + X_L + R
Z_T = $\frac{1}{ωC}$ + ωL + R
Z_T = $\frac{1}{2∏*100Hz*100μC}$ + 2∏*100Hz*5mH + 5Ω
Z_T = 15.91Ω + 3.14Ω + 5Ω
Z_T = 24.05 Ω

Z_X = 15.91Ω + 3.14Ω
Z_X = 19.05Ω

V_OUT = $\frac{ZX}{ZT}$ * V_IN
V_OUT = $\frac{24.05Ω}{19.05Ω}$ * 10*√2*sinωtV
V_OUT = 1.26 * 10*√2*sinωtV

Things are starting to make sense again, and I got to say, I really enjoy doing this. Progress is king.

Assuming some of the above work is correct, I have a couple of questions. t is the time constant of the sinus wave. When t is 0, the voltage is 0. Should my answer then be V_OUT(t) = 17.82sinωtV ?

t is the time variable for the time-domain representation of the voltage (or current) waveform. If 17.82V turns out to be magnitude of the voltage waveform at the output, then you'll write it as you did, but the sin function will also have a phase angle since the reactive components will impose a phase shift. So, supposing A is the magnitude and $\phi$ the phase angle:

$V_{out} = A \ sin(ω t + \phi)$

Also, isn't AC voltage/current given in complex numbers? Sorry for the stupid questions. Hopefully I'll get back into this soon enough :)

Yup. You'll want to take another look at your calculations and use complex values for the impedances.

 

[Mutaja]

When I implement j to my equations, I get:

Z_T = j 15.91Ω + j 3.14Ω + 5Ω

I add the complex numbers together, and convert to polar form:

19.695Ω 75.29°.

When I want to find Z_X, I subtract 5Ω from the equation, and end up with arctan(19.05/0).

Where am I going wrong now?

Edit: I will have another attempt soon.

X_L = jωL = j3.14Ω
X_C = $\frac{1}{jωC}$ = -j15.91Ω

Z_T = 5Ω -j12.77Ω -> 13.714Ω - 68.6175°

Z_X = -j12.77Ω -> 12.77Ω -90°

V_OUT $\frac{ZX}{ZT}$ * V_IN

$\frac{12.77 -90°}{13.714 -68.6175°}$ * 10√2sinωtV

V_OUT = 0.91*10√2sin(ωt - 21.38°)
V_OUT = 12.87sin(ωt - 21.38°)

Am I onto something here?

 

[gneill]

When I implement j to my equations, I get:

Z_T = j 15.91Ω + j 3.14Ω + 5Ω

Whoops. Check the value for the capacitor impedance. Note that a capacitor has a negative impedance (the "j" is in the denominator of the impedance calculation, so when it's promoted to the numerator it changes sign).

The rest of your calculations look okay (at a glance) at least as far as procedure goes. Redo them with the new capacitor impedance value.

 

[Mutaja]

Whoops. Check the value for the capacitor impedance. Note that a capacitor has a negative impedance (the "j" is in the denominator of the impedance calculation, so when it's promoted to the numerator it changes sign).

The rest of your calculations look okay (at a glance) at least as far as procedure goes. Redo them with the new capacitor impedance value.

I'm pretty sure I did that. My edit is somewhat hidden.

There are a couple of "thinkers" attached to this problem. Those are resonance frequency, band width and power limits for R within BW. These are just small problems we should consider, but don't have to do. I've given it a try regardless, and here's what I ended up with:

Resonance frequency:

f_R = $\frac{1}{2∏√(LC)}$
= 225hZ

Band width: f_C2-f_C1 = $\frac{R}{2∏L}$
= 159.15

Power limits: I have no idea about this one as it's supposed to be within my BW. My BW is a given constant. It has no range of values.

This isn't very important, I just wanted to make sure I've touched upon it. If you have any guidance, I'd appreciate it as always.

Thanks a bunch for your help with the above problem regardless. I probably would've lost interest for this subject if it weren't for this forum. Now it's my favorite one.

 

[gneill]

I'm pretty sure I did that. My edit is somewhat hidden.

Okay, well I only saw the version where the capacitive impedance was given as j15.91Ω , which threw off your impedance magnitude and angle, and hence the remainder of the calculations. If you've fixed that, no problem. But I can't check what I can't see

There are a couple of "thinkers" attached to this problem. Those are resonance frequency, band width and power limits for R within BW. These are just small problems we should consider, but don't have to do. I've given it a try regardless, and here's what I ended up with:

Resonance frequency:

f_R = $\frac{1}{2∏√(LC)}$
= 225hZ

Band width: f_C2-f_C1 = $\frac{R}{2∏L}$
= 159.15

Power limits: I have no idea about this one as it's supposed to be within my BW. My BW is a given constant. It has no range of values.

This isn't very important, I just wanted to make sure I've touched upon it. If you have any guidance, I'd appreciate it as always.

Your resonant frequency and bandwidth calculations look okay.

Not sure what they mean by "power limits", unless the components (the resistor in particular) have power ratings.

Thanks a bunch for your help with the above problem regardless. I probably would've lost interest for this subject if it weren't for this forum. Now it's my favorite one.

Good to hear!

 

[Mutaja]

Not sure what they mean by "power limits", unless the components (the resistor in particular) have power ratings.

My problem statement ask for this:

Calculate the upper and lower (max and min) power limit for R, if the frequency is within BW.

Power limit might be a bad translation on my part, as I can't find anything in my book regarding this.

No biggie, though. I will ask my lecturer after our spring break :)

 

[gneill]

My problem statement ask for this:

Calculate the upper and lower (max and min) power limit for R, if the frequency is within BW.

Power limit might be a bad translation on my part, as I can't find anything in my book regarding this.

No biggie, though. I will ask my lecturer after our spring break :)

Okay, so it looks like you'll need to find the minimum and maximum RMS output voltage between the bandwidth frequency limits. Use this with the known resistance value to find the powers.

You should be able to use knowledge of what happens to the reactive impedance at resonance and the definition of cutoff (or corner) frequency as shortcuts.