Solving Advanced SHM Problem: Tips & Guidance

[PhysicsKid0123]

I have a homework problem I need help with. I don't want the answer given to me since I know I can answer it with the proper guidance.
How should I approach this problem?

This is what I have so far. How should I approach this? Did I start off right?

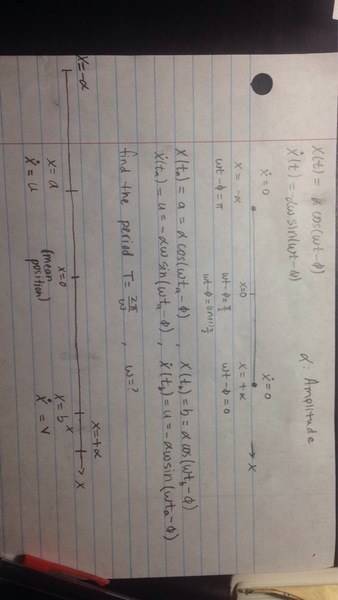
Thanks in advanced!

 

[PhysicsKid0123]

Sorry thought this was the homework section

 

[davenn]

hi there

can you please rotate and repost your images so I don't have to lie down to try and read them :)

cheers
Dave

PS have asked for it to be moved to homework section

 

[ShayanJ]

We have:
x=\alpha \cos{(\omega t-\phi)} \Rightarrow \dot x=-\alpha \omega \sin{(\omega t-\phi)}
Let's take \delta=\omega t-\phi, then we can write:
\sin^2 \delta+\cos^2 \delta=1 \Rightarrow (\frac{\dot x}{\alpha \omega})^2+(\frac{x}{\alpha})^2=1.
Is it enough or I should explain further?

 

[PhysicsKid0123]

We have:
x=\alpha \cos{(\omega t-\phi)} \Rightarrow \dot x=-\alpha \omega \sin{(\omega t-\phi)}
Let's take \delta=\omega t-\phi, then we can write:
\sin^2 \delta+\cos^2 \delta=1 \Rightarrow (\frac{\dot x}{\alpha \omega})^2+(\frac{x}{\alpha})^2=1.
Is it enough or I should explain further?

Mhmm let me see what I can extrapolate from this. Give me a moment... Thanks btw.

 

[PhysicsKid0123]

hi there

can you please rotate and repost your images so I don't have to lie down to try and read them :)

cheers
Dave

PS have asked for it to be moved to homework section

Okay! I will take a better picture!

 

[Drakkith]

Since this has been reposted in the HW section, I will close this thread.