Solving an equation for ##x## involving inverse circular functions

[brotherbobby]

Homework Statement

Solve the following equation : $\pmb{\tan^{-1}\frac{1-x}{1+x}=\frac{1}{2}\tan^{-1}x}$

Relevant Equations

1. If $\tan\theta=1\Rightarrow \theta =\tan^{-1} 1 = \tfrac{\pi}{4}$, $\underline{\text{the principal value}}$.
2. $\tan(A-B) = \frac{\tan A - \tan B}{1+\tan A \tan B}$

Problem Statement : Solve for $x$ :

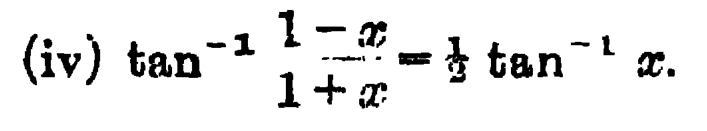
Attempt : If I take $x=\tan\theta$, the L.H.S. reads $$\tan^{-1}\frac{1-\tan\theta}{1+\tan\theta}= \tan^{-1}\left[\tan\left(\frac{\pi}{4}-\theta \right) \right ]=\frac{\pi}{4}-\theta.$$

On going back to $x$ from $\theta$, the given equation now reads : $$\frac{\pi}{4}-\tan^{-1}x = \frac{1}{2}\tan^{-1}x\Rightarrow \tan^{-1}x=\frac{2}{3}\times \frac{\pi}{4}=\frac{\pi}{6}\Rightarrow \boxed{x=\frac{1}{\sqrt{3}}}.$$

Answer : I copy and paste the answer from the book :

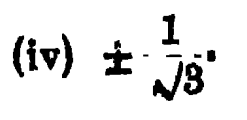
Doubt : Where does the answer $-\frac{1}{\sqrt{3}}$ come from? If we take the principal value of $\tan^{-1}1=\dfrac{\pi}{4}$, I don't see how there can be a second answer.

A hint or suggestion will be welcome.

 

[Mark44]

I can't work through this at the moment. What I would do is to check whether $-\frac 1{\sqrt 3}$ is a solution of the original equation. If not, the book's answer is a typo.

 

[PeroK]

Attempt : If I take $x=\tan\theta$, the L.H.S. reads $$\tan^{-1}\frac{1-\tan\theta}{1+\tan\theta}= \tan^{-1}\left[\tan\left(\frac{\pi}{4}-\theta \right) \right ]=\frac{\pi}{4}-\theta.$$

Note that $\tan^{-1}\tan x = x$ only when $x \in (-\frac \pi 2, \frac \pi 2)$

 

[PeroK]

Although, in this case this subtlety does not produce a second solution.

 

[PeroK]

I did a bit of investigating. If we try: $$\tan^{-1}\frac{1-x}{1+x} = k\tan^{-1}x$$then we always get one solution (for $k > -1$). And, we get a second solution for $\frac 1 2 < k < 2$.

There is almost a second solution for $k = \frac 1 2$, which is $x \rightarrow -\infty$, or $\theta = -\frac \pi 2$.

 

[Mark44]

I think there's a typo in the answer for $x = -\frac 1 {\sqrt 3}$
From Excel, with that value, $\arctan(\frac{1 - x}{1 + x}) \approx 1.308997$, while $.5\arctan x \approx -0.2618$.

 

[PeroK]

I think there's a typo in the answer for $x = -\frac 1 {\sqrt 3}$
From Excel, with that value, $\arctan(\frac{1 - x}{1 + x}) \approx 1.308997$, while $.5\arctan x \approx -0.2618$.

Try $x$ large and negative instead!

 

[Mark44]

Try x large and negative instead!

I was just comparing the two posted solutions.

 

[PeroK]

I did a bit of investigating. If we try: $$\tan^{-1}\frac{1-x}{1+x} = k\tan^{-1}x$$then we always get one solution (for $k > -1$). And, we get a second solution for $\frac 1 2 < k < 2$.

There is almost a second solution for $k = \frac 1 2$, which is $x \rightarrow -\infty$, or $\theta = -\frac \pi 2$.

Just to correct this after having double-checked everything. $x = \tan \theta$ is a solution, where
$$\theta = \frac{\pi}{4(k+1)} \ \ (k < -2 \ or \ k > -\frac 1 2)$$ $$\theta = \frac{-3\pi}{4(k+1)} \ \ (\frac 1 2 < k < 2)$$ And we have two solutions when $\frac 1 2 < k < 2$. For example, with $k = 1$ we have:
$$\theta = -\frac{3\pi}{8} \ and \ \theta = \frac{\pi}{8}$$

 

[PeroK]

PS I think you learn a lot more about these equations by working out the general case, than doing one problem with a specific value of $k = \frac 1 2$ and then moving on.

 

[vela]

I think there's a typo in the answer for $x = -\frac 1 {\sqrt 3}$
From Excel, with that value, $\arctan(\frac{1 - x}{1 + x}) \approx 1.308997$, while $.5\arctan x \approx -0.2618$.

The difference between those two values is $\pi/2$. It looks like they're getting a second solution from
$$\frac \pi 4 - \theta = \frac 12 (\theta + \pi),$$ which implies $\theta = -\frac \pi 6$.

 

[PeroK]

The difference between those two values is $\pi/2$. It looks like they're getting a second solution from
$$\frac \pi 4 - \theta = \frac 12 (\theta + \pi),$$ which implies $\theta = -\frac \pi 6$.

And the problem with that is that it requires $\frac \pi 4 - \theta < -\frac \pi 2$. Which requires $\theta > \frac{3\pi}{4}$. That would give the equivalent solution of $\theta = \frac{5\pi}{6}$. But, when we set up $x = \tan \theta$ we needed a single range for $\theta$, such as $\theta \in (-\frac \pi 2, \frac \pi 2)$.

In other words, solutions with $\theta$ outside this range must be excluded.

Note that in general we may have $\frac \pi 4 - \theta > \frac \pi 2$, which happens if $-\frac \pi 2 < \theta < -\frac \pi 4$. That's why we get a second solution for some values of $k$.

Ironically, the book got the completely wrong solution $\theta = -\frac \pi 6$, but missed the near solution $\theta = -\frac \pi 2$, which equates to infinitely large negative $x$.

 

[brotherbobby]

Thank you all for your comments. I am the creator (OP) of this thread and I lost most of what you said towards the end. For now I respond to @Mark44 's post #2 :

What I would do is to check whether $-\tfrac{1}{\sqrt{3}}$is a solution of the original equation. If not, the book's answer is a typo.

Problem Statement : Solve the equation :

Attempt : I have solved the problem in my post #1 above. I got the answer $\boxed{x = \tfrac{1}{\sqrt{3}}}$.

Issue : The text gives the answer : $\pmb{x = \pm \frac{1}{\sqrt{3}}}$. Where does it get the answer $x=-\tfrac{1}{\sqrt{3}}$ from, when we know that the principal value of $\tan^{-1}(1) = \tfrac{\pi}{4}$? (see my solutions in post#1 above).

Resolution : Let me put $x=-\tfrac{1}{\sqrt{3}}$ on both sides of the equation to see if the answers match.

L.H.S. = $\tan^{-1}\frac{1+\frac{1}{\sqrt{3}}}{1-\frac{1}{\sqrt{3}}}= \tan^{-1}\frac{\sqrt{3}+1}{\sqrt{3}-1}=-\tan^{-1}\frac{1+\sqrt{3}}{1-\sqrt{3}}=-\tan^{-1}\left[ \tan\left(\pi/4+\pi/3 \right) \right]=-7\pi/12$.

R.H.S. = $\frac{1}{2}\tan^{-1}\left(-\frac{1}{\sqrt{3}}\right)=-\frac{1}{2}\tan^{-1}\frac{1}{\sqrt{3}} = -\frac{1}{2}\times\frac{\pi}{6} = -\pi/12.$

Clearly the two sides are different when $x = -1/\sqrt 3$, unless I am mistaken in my workings above.

That should be enough to rule out $x = -1/\sqrt 3$ as a solution to the given equation.

 

[brotherbobby]

Note that $\tan^{-1}\tan x = x$ only when $x \in (-\frac \pi 2, \frac \pi 2)$

I did not understand, so if you can explain.

Isn't it always the case that $\tan (\tan^{-1}x) = x$, irrespective of the value of $x$?

Of course I am aware that $\tan \pi/2$ blows up.

 

[PeroK]

I did not understand, so if you can explain.

Isn't it always the case that $\tan (\tan^{-1}x) = x$, irrespective of the value of $x$?

Of course I am aware that $\tan \pi/2$ blows up.

Yes, $\tan (\tan^{-1}x) = x$. But, $\tan^{-1} (\tan x) = x$ only when $x \in (-\frac \pi 2, \frac \pi 2)$

 

[PeroK]

That should be enough to rule out $x = -1/\sqrt 3$ as a solution to the given equation.

Yes, the book is wrong. But, likewise, you potentially missed a second solution. In this case, $\theta = -\frac \pi 2$ is a solution of sorts.