Solving an ODE-45 from Euler-Lagrange Diff. Eqn.

[Axecutioner]

I need to find the equation of motion of a double pendulum, as shown here:

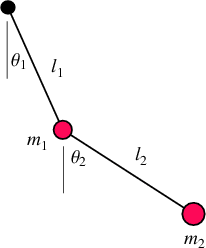
I've gotten as far as the two euler-lagrange differential equations, simplified to this:

K₁\ddot{θ}₁ + K₂\ddot{θ}₂cos(θ₁ - θ₂) + K₃\dot{θ}₂²sin(θ₁ - θ₂) + K₄sin(θ₁) = 0
K₅\ddot{θ}₂ + K₆\ddot{θ}₁cos(θ₁ - θ₂) + K₇\dot{θ}₁²sin(θ₁ - θ₂) + K₈sin(θ₂) = 0

Assuming initial conditions \ddot{θ}_1o, \dot{θ}_1o, θ_1o, \ddot{θ}_2o, \dot{θ}_2o, θ_2o

What would these equations of motion be?
θ₁(t) =
θ₂(t) =

I was told it could be done in MATLAB but I don't have the software or know how to use it yet so any help would be appreciated. Step-by-step solution would be even better. Thanks in advance.

 

[dikmikkel]

Have you considered the rotational energy aswell? You have to have a moment of inertia dependent term.
The procedure for solving this type of problems is as follows:
1. Define your generalized coordinates for each of the masses: e.g. (x1,y1) = (l1sin(theta(t),l1cos(theta(t)) ...
2. Find the velocity and simplify it. Remember the chain rule for differentiation.
3. Find the Potential energy V and kinetic T(T = 1/2m_1v_1^2+1/2m_2v_2^2+1/2I_1 \omega_1^2+1/2I_2\omega_2^2) where omega = dtheta/dt
and the lagrangian is L = T-V
4. Write down your dynamical equations, 2 masses gives 2 equations. and there you go.
\dfrac{\partial L}{\partial \theta_1} - \dfrac{d}{dt}\dfrac{\partial L}{\partial \dot{\theta_1}}=0
Summary: Be strict defining coordinate system. Remember the chain rule and product rule for differentiation. Concentrate it is hard algebra.
The equations of motion comes from solving this differential equation system. Sometimes it is assumed that sin(theta) = theta for theta<<1 and that simplifys a lot.
But in general this problem is chaotic in nature, and you would probably solve nummericaly in matlab.

 

[Axecutioner]

Here's what I've done so far, before I posted the OP:

http://i.imgur.com/c1Sdb.jpg

Some of the K values are the same but just keep each one different, since this entire double pendulum case is a simplification of part of a project I'm working on.

And Rotational Kinetic energy and Kinetic energy are the same for a point mass ( 1/2mv^2 = 1/2mL^2w^2 = 1/2Iw^2) so adding both would be wrong.

And I do not want to use the small angle approximation because the actual pendulum in my project is being torqued with an angle dependent force, and the angles involved cover a wide range.

 

[dikmikkel]

Iv'e tried solving the system in maple nummerically without luck. I don't think i am able to get an analytical solution, sorry. And I've never seen a analytical solution.