Solving Car Suspension Modeling: Understanding Input Forces and Movement Types

[Lord Doppler]

Homework Statement

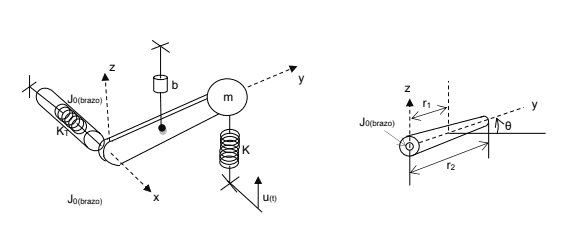
Find the mathematic model of car suspension, express the movement equations in differential equations U(t)

Relevant Equations

F = ma
T = Ja

Hello, I'm trying to solve this problem but I'm confused with some things, is correct that in the system there are two input forces, the torque and u(t)? I assumed that the system has two free levels, which are the z displacement and theta (rotational movement), so the system has a linear movement and a rotational movement? Besides the KT spring inside of the arm how I can intepret it? I'm not sure how to board this problem

 

[jack action]

is correct that in the system there are two input forces, the torque and u(t)?

There is also the damping force from element $b$.

I assumed that the system has two free levels, which are the z displacement and theta (rotational movement), so the system has a linear movement and a rotational movement?

Just the rotational movement. The linear movement you are referring to is a direct consequence of the rotation.

Besides the KT spring inside of the arm how I can intepret it?

It is a torsional spring. $K_T$ would be the torsional stiffness which links the torque and the angular displacement.

 

[Lnewqban]

It seems to me that the only input force to the system is U.
That input makes the two parts of the system oscilate:
1) The mass-less pivoting arm with the mass m, onto which U is acting vertically.
2) The torsion bar, which acts as a spring and having rotational inertia.

You can consider the points represented by a cross to be common fixed points, all interconnected via chassis of the car.

The damper is located at distance r1 from the pivot, so its effect on stopping m should be reduced (respect to a classical oscillating spring-damper system).
The given angle also reduces the effect of U about the pivot and torsion bar.

The effect of the torsional and linear resistances or springs should be added up, as they seem to be working in series rather than in parallel.

 

[Lord Doppler]

It seems to me that the only input force to the system is U.
That input makes the two parts of the system oscilate:
1) The mass-less pivoting arm with the mass m, onto which U is acting vertically.
2) The torsion bar, which acts as a spring and having rotational inertia.

You can consider the points represented by a cross to be common fixed points, all interconnected via chassis of the car.

The damper is located at distance r1 from the pivot, so its effect on stopping m should be reduced (respect to a classical oscillating spring-damper system).
The given angle also reduces the effect of U about the pivot and torsion bar.

The effect of the torsional and linear resistances or springs should be added up, as they seem to be working in series rather than in parallel.

I agree when you say that U is the only input force, but there is no a torque T also? Like input force I mean

 

[Lnewqban]

Yes, the torsional bar will never see what is causing the torque that it has to resist.
That torque is the combination of U and horizontal projection of the arm’s length r2.
Note that directions of U and distance about the torsion bar must be perpendicular for proper calculation.
Same applies for resistive force of damper b.

 

[Lord Doppler]

Yes, the torsional bar will never see what is causing the torque that it has to resist.
That torque is the combination of U and horizontal projection of the arm’s length r2.
Note that directions of U and distance about the torsion bar must be perpendicular for proper calculation.
Same applies for resistive force of damper b.

Thanks!