- #1
warhammer
- 158
- 31
- Homework Statement
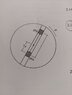
- A disk rotates with constant angular velocity ω. Two masses A & B slide without friction in a groove passing through center of disk. They are connected by string of length 'l' and are initially held in position by catch with mass A at a distance r(A) from the center. Neglect gravity. At t=0 the catch is removed and masses are free to slide. Find r''(A) immediately after catch is removed in terms of A,B,l,r(A) & ω.
- Relevant Equations
- F(A)-T=m(A)*r''(A)
T-F(B)=m(B)*r''(B)
r(A)+r(B)=l
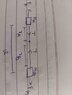
I am also attaching picture of the figure as well as my diagram to showcase the forces.
I have devised these equations because as per the question, r(A) is acting like a reference.
The constraint r(A)+r(B)=l--------(i) transforms to r''(B)= - r''(A) ------- (ii)
Using-
F(A)-T=m(A)*r''(A)
T-F(B)=m(B)*r''(B)
Adding both & using (i) & (ii), F(A)-F(B)= r''(A) {m(A)-m(B)}
r(A)*ω^2 [m(A)+m(B)] - m(B)*l*ω^2= r''(A) {m(A)-m(B)}
{ r(A)*ω^2 [m(A)+m(B)] - m(B)*l*ω^2} /{m(A)-m(B)}
This answer is not coming out to be correct. I sense I have taken force directions wrong but unable to understand why.
I have devised these equations because as per the question, r(A) is acting like a reference.
The constraint r(A)+r(B)=l--------(i) transforms to r''(B)= - r''(A) ------- (ii)
Using-
F(A)-T=m(A)*r''(A)
T-F(B)=m(B)*r''(B)
Adding both & using (i) & (ii), F(A)-F(B)= r''(A) {m(A)-m(B)}
r(A)*ω^2 [m(A)+m(B)] - m(B)*l*ω^2= r''(A) {m(A)-m(B)}
{ r(A)*ω^2 [m(A)+m(B)] - m(B)*l*ω^2} /{m(A)-m(B)}
This answer is not coming out to be correct. I sense I have taken force directions wrong but unable to understand why.
Attachments
Last edited by a moderator: