Solving Equilibrium w/ Plank & Forces | Physics Problem

[ago01]

Homework Statement

A heavy, 6m long uniform plank has a mass of 30 kg. It is positioned so that 4m is supported on the deck of a ship and 2m sticks out over the water. It is held in place only by its own weight. You have a mass of 70kg and walk the plank past the edge of the ship.

Relevant Equations

Torque, Forces in Y, Forces in X. Static equilibrium.

I first created the following diagram (after watching some videos, I had initially combined masses and this is wrong).

$F_p$ Is the gravitational force of the board on the boat.
$N_0$ Is the corresponding normal force the board experiences from the boat.
$F_m$ Is the force of me at the point I step over the pivot.
$N_1$ Is the normal force I experience from the plank after the pivot.

$m_p = 30 kg$
$m_m = 70 kg$

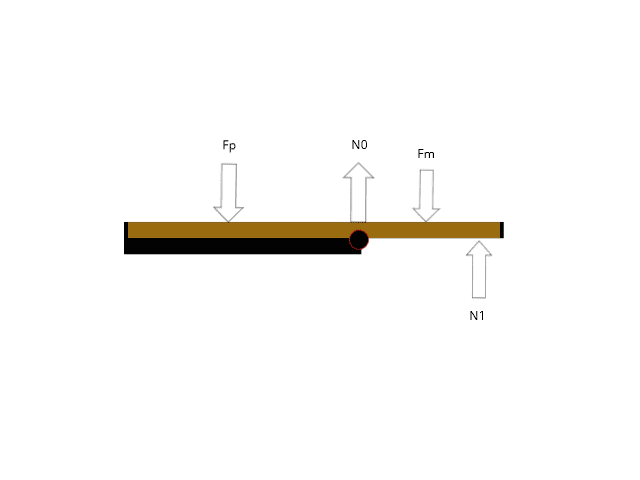
The pivot point is the red outlined black dot. The point exactly where the plank begins to overhang.

If this is in static equilibrium then at any point after the pivot that doesn't cause the plank to rotate I must be experiencing some normal force from the plank as well.

So, using the static equilibrium equations:

$\sum{F_x} = 0$

$\sum{F_y} = N_0 + N_1 - m_pg - m_mg = 0$

$\sum{T} = 0$

Call the left end of the plank $A$ and where I am standing $B$:

$T_{A} = -4m_pg$
$T_{B} = -rm_mg$
$T_{N_0} = 0$ (since it is at the lever arm)
$T_{N_1} = rN_1$ (since this torque counters my torque in equilibrium).

So $\sum{T} = -4m_pg - rm_mg + rN_1 = 0$

I understand that in order for the board to rotate it must be the case that $N_1$ = 0. But if that's the case, solving for $N_0$ using the sum of the y-forces does not help me solve for $r$ since in this case $T_{N_1} = 0$ and so:

$-4m_pg = rm_mg$

$r = -1.71m$

Which is obviously wrong. I'm sure I'm staring right at the answer and missing a critical piece of insight to solve this.

 

[Lnewqban]

N1 does not exist as the normal force you experience from the plank after the pivot.

N0 Is the corresponding normal reaction force the board experiences from the boat at the pivot point when tipping over is imminent.

For creating a good FBD, you should not consider the internal forces of the system, like the action-reaction forces among your feet and board.

Please, see
https://en.wikipedia.org/wiki/Free_body_diagram

https://www.physicsforums.com/threads/18-free-body-diagrams-statics.679262/

As the board is uniform in shape and thickness, you can consider the 30 kg as concentrated in its middle point, 3 m from each end.

 

[ago01]

N1 does not exist as the normal force you experience from the plank after the pivot.

N0 Is the corresponding normal reaction force the board experiences from the boat at the pivot point when tipping over is imminent.

For creating a good FBD, you should not consider the internal forces of the system, like the action-reaction forces among your feet and board.

Please, see
https://en.wikipedia.org/wiki/Free_body_diagram

https://www.physicsforums.com/threads/18-free-body-diagrams-statics.679262/

As the board is uniform in shape and thickness, you can consider the 30 kg as concentrated in its middle point, 3 m from each end.

I finally figured it out but I'm left a little confused at why we don't consider the weight of the board and person together. To solve it I needed to consider the center of mass and it's behavior (which is where the gravitational force of the board rests). I would think that this mass would be $M_m + M_p$ but I was wrong.

Defining the system is a little confusing here, mostly because you are looking at the board + person but treating them separately.

 

[Lnewqban]

If you consider the plank-man as a solid system, then you first must find the center of mass of each body, in order to find the combined center of mass of the plank-man system.

Please, see:
https://efcms.engr.utk.edu/ef151-2019-08/sys.php?f=bolt/bolt-main&c=class-4-1&p=area

If that combined system’s center of mass is located left of the pivot, it induces a CCW moment: the system will remain still because it does not have freedom of rotation in that direction.
If that combined system’s center of mass is located right of the pivot, it induces a CW moment: the system will rotate and fall because it has freedom of rotation in that direction.

 

[sysprog]

It seems to me that if the system is static, (the man walking the plank freezes and the sword hasn't yet prodded him), and we pretend that the plank has the same density as the man has (probably really the man is somewhat denser) we say thanks to Euclid and find the centroid, and then when the sword prods, and the system becomes dynamic (the prodded man starts walking), we says thanks to Newton and Leibniz (and other luminaries) and start figuring derivatives (fluxions), but I think that @Lnewqban is right about the pivot point.

 

[haruspex]

I finally figured it out but I'm left a little confused at why we don't consider the weight of the board and person together. To solve it I needed to consider the center of mass and it's behavior (which is where the gravitational force of the board rests). I would think that this mass would be $M_m + M_p$ but I was wrong.

Defining the system is a little confusing here, mostly because you are looking at the board + person but treating them separately.

As @Lnewqban notes, you cannot simply add the masses because their mass centres are at different horizontal positions, so have different torque arms about the pivot.
Indeed, it is generally unhelpful to find the common mass centre of a composite system. Most such problems are more easily solved considering the masses separately. This is particularly so for moment of inertia questions.

 

[sysprog]

As @Lnewqban notes, you cannot simply add the masses because their mass centres are at different horizontal positions, so have different torque arms about the pivot.
Indeed, it is generally unhelpful to find the common mass centre of a composite system. Most such problems are more easily solved considering the masses separately. This is particularly so for moment of inertia questions.

Is the walking the plank problem being considered in 3 spatial dimensions here? I was looking at downward (gravity) and forward (along the plank). I disregarded sidelong.

 

[sysprog]

Thanks to @berkeman.