Solving Euler's Dynamics Equations for a Gyro-Compass

[curiousPep]

Hello,
I know it might sound silly but sometimes I get confused.
Let's say I have a gyro-compass and I get 3 equations of torque for the 3 axes.
I am expected to find the equation of motion and two of them are equated with 0.

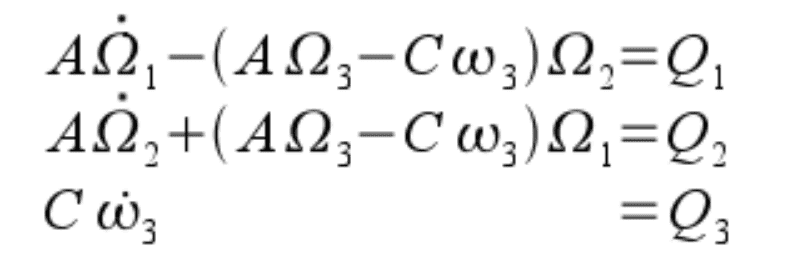
These are the Euler's dynamics equation with moving reference frame (gyroscope equation)
I get that both Q2 and Q3 are equal to 0 and Q1 not equal to 0.
Hence, it is easier to use the equation of Q2 and Q3, but by inspection, these two don't give the same equation.
So what are the criteria to decide which one will give the equation of motion of the gyro-compass?

 

[LightHero]

The criteria for deciding which equation to use in order to find the equation of motion of the gyro-compass depends on the type of motion you are interested in studying. If you are trying to study linear motion, then you will likely use the equation of Q1. If you are studying rotational motion, then you may use either Q2 or Q3 depending on the type of rotation you are interested in. In addition, you may also need to consider the physical constraints of the system, such as the direction of the applied torque and any external forces that may be acting on the system.