Solving for 'a' with Torque, Force, and Mass Moment of Inertia

In summary, the conversation discusses solving for the mass moment of inertia of a wheel using the equations for torque and mass moment of inertia. The solution provided does not seem to take into account the effects of gravity and tension from a rope attached to the wheel. A free body diagram is also mentioned as necessary for properly solving the problem.
  • #1
haven
7
0
Homework Statement
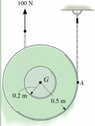
The 7.80 kg spool has a radius of gyration of 0.320 m and rolls without the ropes slipping. The ropes have negligible mass.

There is also a force pulling the spool upward at 100N and the outer radius is 0.5 and the inner radius is 0.2-shown in picture
Let up be the positive y-direction and CCW be the positive rotational direction.
Assume 3 SF for all givens.
Relevant Equations
Torque = I*a
Io=m*ro^2
What I did was plug in the outer radius time the force into the torque and then the mass moment of inertia is equal to m*ro^2 so then I plugged in the mass times the radius of gyration squared into I and solved for a but this is not right.
 

Attachments

  • Screen Shot 2022-11-27 at 6.14.19 PM.png
    Screen Shot 2022-11-27 at 6.14.19 PM.png
    37.8 KB · Views: 90
Physics news on Phys.org
  • #2
Is there a figure that comes with this? If so, please post it using the "Attach files" link, lower left.
 
  • #3
kuruman said:
Is there a figure that comes with this? If so, please post it using the "Attach files" link, lower left.
yes I just attached it^^
 
  • #4
Thank you for posting the figure. Draw a free body diagram (FBD) of the wheel.

Note that the center of the wheel has a linear acceleration and there is also angular acceleration about the center of the wheel. So you need to write two equations, one for the linear acceleration and one for the angular acceleration. Don't forget the tension in the rope that is attached to the ceiling; it too exerts a force and a torque on the wheel. Gravity also affects the motion and your solution does not seem to have taken it into account.
 

FAQ: Solving for 'a' with Torque, Force, and Mass Moment of Inertia

How do I calculate the value of 'a' in a torque equation?

To solve for 'a' in a torque equation, you need to have the values for force, mass moment of inertia, and the distance between the pivot point and the point where the force is applied. You can then use the equation 'a = (T - I*α)/r', where T is the torque, I is the mass moment of inertia, α is the angular acceleration, and r is the distance. Rearrange the equation to solve for 'a'.

What is the significance of 'a' in a torque equation?

'a' represents the linear acceleration of an object in a rotational motion. It is the distance from the pivot point to the point where the force is applied multiplied by the angular acceleration. The value of 'a' determines how quickly the object will rotate and how much force is required to achieve that rotation.

Can 'a' have a negative value in a torque equation?

Yes, 'a' can have a negative value in a torque equation. This indicates that the object is rotating in the opposite direction of the applied force. The negative sign is important to consider when calculating the direction of the torque and the resulting motion of the object.

How does the mass moment of inertia affect the value of 'a' in a torque equation?

The mass moment of inertia is a measure of an object's resistance to rotational motion. The larger the value of I, the more force is required to achieve a certain angular acceleration. Therefore, a larger mass moment of inertia will result in a smaller value of 'a' for the same torque and force values.

Can I use the same equation to solve for 'a' in all types of torque problems?

While the basic equation 'a = (T - I*α)/r' can be used to solve for 'a' in most torque problems, there are some situations where additional factors may need to be considered. For example, in cases where the object is not a point mass, the moment of inertia may need to be calculated using the parallel axis theorem. Additionally, in dynamic situations, the torque and angular acceleration may vary over time, requiring the use of calculus to solve for 'a'.

Similar threads

What is the "r" in the moment of inertia?
Replies
13
Views
2K
Calculating Moment of Inertia for Hollow Cylinder w/ Water
2
Replies
40
Views
4K
How Does Torque Affect Angular Acceleration in a Circular Disk?
Replies
8
Views
2K
Moment of inertia of a disk about an axis not passing through its CoM
Replies
11
Views
2K
Angular acceleration of plank hanging off edge with a weight
Replies
7
Views
963
How Does Angular Momentum Conservation Affect Asteroid Collision Dynamics?
10
Replies
335
Views
11K
Correct Use of the Parallel Axis Theorem for Moment of Inertia
Replies
2
Views
1K
Mass moment of inertia of a composite shape
Replies
5
Views
3K
Moment of Inertia with pulley and two masses on a string (iWTSE.org)
Replies
8
Views
9K
Moment of Inertia of a sphere about an axis
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top