Solving for Angular Velocity After a Disc Collision

[daavid]

TL;DR Summary

angular velocity of two discs after collision

Hello to everyone, first of all shame on me I has to ask and can not figure out it by myself...
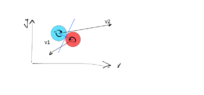
The problem is I am trying to code game where two homogenous discs with same mass and same diameter, no fricition due to gravitational forces, can collide.

I can figure out the speed and direction after collision for both objects without any problem however I do not know how to calculate the final angular velocity after the collision. Collision is pure 2D and 100% elastic. I think I can say there is no friction between those two discs (I suppose there still will be change in angular velocity even without friction between those two discs).

At the moment of the collision
v1x, v1y, v2x, v2y, θ1, θ2 (movement angles), ϕ contact angle are known.

If someone could show me formula with some example I would be extremely grateful.

 

[Filip Larsen]

I think I can say there is no friction between those two discs (I suppose there still will be change in angular velocity even without friction between those two discs)

If you are having zero friction between two colliding discs then how do you see them exchange angular momentum? To change angular velocity a disc must experience forces along its (elastic) contact surface that sums up to have a transverse (non-radial) direction and without friction that is going to require some kind of asymmetric shaped contact surface.

Perhaps if you explain what you are trying to model with the discs and their interaction it will be easier for people here to provide for some relevant help.

 

[kuruman]

I think OP meant to say that, while the discs are in contact, there is no sliding of one surface relative to the other.

 

[Baluncore]

I can figure out the speed and direction after collision for both objects without any problem however I do not know how to calculate the final angular velocity after the collision. Collision is pure 2D and 100% elastic.

I think you must follow through the mechanism of the interaction as three satates, connected by two steps.

State 1. The two discs are initially spinning independently. The discs have linear and angular momentum and energy. They collide at an instant.

State 2. Maybe the rims of the two discs are instantly fused on contact to make a dumbbell with a centre of mass and a different moment of inertia. The dumbbell centroid has a linear velocity. The dumbbell also has a rotation about it's centroid.

State 3. The discs then separate, each with a share of the linear and angular momentum.

 

[kuruman]

State 3. The discs then separate, each with a share of the linear and angular momentum.

$\dots~$ and energy.

 

[Baluncore]

… and energy.

Obviously, if there is to be a valid solution, the energy account must balance.

It appears to be the definition of state 2, that transforms state 1 into state 3, that represents the crux of this problem. Once we understand that momentary middle state the problem can be solved.

I do wonder how the OP defines or describes the system at the instant of state 2.

 

[daavid]

I think OP meant to say that, while the discs are in contact, there is no sliding of one surface relative to the other.

exactly

 

[kuruman]

Summary:: angular velocity of two discs after collision

v1x, v1y, v2x, v2y, θ1, θ2 (movement angles), ϕ contact angle are known.

I would assume that v1x, v1y, v2x, v2y, θ1, θ2 are written relative to axes fixed in space. Are they the velocities and angles just before the collision? If so, the relevant direction is the center to center (CTC) direction because linear momentum is transferred in that direction only. That's the easy part. Doing Step 2 in @Baluncore's post #4 requires some thought. One thing that is not clear to me is "ϕ contact angle". Where is it measured from, i.e. when is it zero, and how do you determine what it is?

 

[Baluncore]

One thing that is not clear to me is "ϕ contact angle". Where is it measured from, i.e. when is it zero, and how do you determine what it is?

Is the contact angle not the normal to the center to center (CTC) direction.

 

[kuruman]

Is the contact angle not the normal to the center to center (CTC) direction.

An angle needs two lines to be defined. One relevant line is the CTC direction. The other relevant line is along the relative velocity vector. My question is whether OP's ϕ is defined using these two directions and, if so, whether ϕ = 0 correspond to a head-on collision or to a glancing collision.

 

[Baluncore]

When two rotating discs contact, (imagine very fine tooth gear wheels mesh), some of the angular momentum of the discs will be converted into linear momentum of the disc centres.

That velocity change will be proportional to the sum of the angular velocities. If they are equal and opposite there will be no effect.

When two non-rotating discs collide, with a glancing blow, the two discs will begin to spin at equal and opposite rates.

 

[kuruman]

When two rotating discs contact, (imagine very fine tooth gear wheels mesh), some of the angular momentum of the discs will be converted into linear momentum of the disc centres.

I know what you mean, but I think it is more appropriate to say that some of the angular momentum will be converted to orbital angular momentum of the disc centers about the point of contact. The linear momentum of the center of mass of the two-disc system, which is at the point of contact during the collision, will of course remain unchanged.

 

[MikeLizzi]

I am doing some programming and will eventually have to deal with this same complicated problem. Here is my take. I'm going to strip it down into 2 manageable pieces.

First, the trivial piece. No rotations. It appears the OP has already solved this version, but I will summarize here.

Consider 2 moving rigid disks of equal mass colliding, not necessarily head on. The image the OP posted shows this nicely.

The easiest way to analyze this problem is to rotate the X-Y Coordinates so that the X-Axis passes thru the centers of both disks. Decompose the velocity vector of each disk so that each has a component along that X-Axis. The other component of velocity for each disk will be along the Y-Axis. Now you have a head-on collision in the X-direction. So after collision, the Y component of each disk will be unchanged. If you respect conservation of Linear Momentum in the X-direction and conservation of total Kinetic Energy of the system then the only X-directed velocity each disk can have after the collision is one of the velocity values from before the collision. They either keep their original X-directed velocity or exchange them. For the disks to keep their original X-directed velocities, they would have to pass thru each other, a valid math solution, but not mechanically allowed. That leaves the only result that they exchange X-directed velocities, they bounce off each other. Recombine the new X and Y velocities to get the total final velocities of each disk. Then rotate those velocities back to the original Coordinate orientation. Anyone who wants to present a mathematically rigorous solution is free to post, but I don't expect it will be different from what I have just concluded.

Now for rotating disks.

Stay with the coordinates where there is a head-on collision in the X-direction. Consider the moment of impact of 2 rotating disks . If there is no friction at the point of impact, 100% sliding, there is no way for one disk to change the rotation of the other. The 2 disks separate with their original angular velocities. I don't think that solution is realistic. If there is enough friction, conservation or Angular Momentum and total Kinetic Energy will require the 2 disks to exchange angular velocities. That solution is more realistic. But, in the real world what really happens, I think, is that there is some friction and some sliding. And that solution is indeterminate.

<Added 2 Hours later>
Ooch !
As I think about the rotation version I realize I screwed up. What I concluded is wrong. Sorry OP. Please disregard. I don't know how to solve this problem!

 

[TonyStewart]

One game that involves friction on contact involves 3D round on a 2D flat surface is billiards, another maybe is air hockey. Don't you want friction in your game?

See here for gear effect in billiards. http://www.physics.usyd.edu.au/~cro... sliding friction,the ball has two components