Solving for Derivative of 2x^3-x^2+cx+d

  • MHB
  • Thread starter Chipset3600
  • Start date
  • Tags
    Derivative
In summary, your teacher wants you to find a point on the curve where the derivative is -2. You can find the point by using the equation and substituting in the values for c and d.
  • #1
Chipset3600
79
0
Hello MHB, please help me solve this problemn.

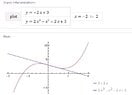
knowing that 2y+4x-6=0 is the equation which is one of the lines tangent to the curve y= 2x^3-x^2+cx+d.
Find the derivative of this function in one of the points of the curve.
 
Physics news on Phys.org
  • #2
What do you require of the derivative and the curve so that the given line is tangent to the curve?
 
  • #3
MarkFL said:
What do you require of the derivative and the curve so that the given line is tangent to the curve?
this implicit function "2y+4x-6=0" is tangent of this curve "y= 2x^3-x^2+cx+d"
the gradient is "-2", but i don't know my C and D. How can i find the common point?
 
  • #4
Equate the derivative of the cubic to -2, and you may express c as a function of x.

Then, substitute for c into the cubic and find where this new function's derivative is equal to -2. You will get 2 x-values. One of these will allow you to then easily find c and d.
 
  • #5
MarkFL said:
Equate the derivative of the cubic to -2, and you may express c as a function of x.

Then, substitute for c into the cubic and find where this new function's derivative is equal to -2. You will get 2 x-values. One of these will allow you to then easily find c and d.

Lets see if i understood: View attachment 453

Is this what you mean??
 

Attachments

  • load.jpg
    load.jpg
    30.4 KB · Views: 41
  • #6
Yes, after substituting for c, then taking the derivative, you have found:

$\displaystyle y'=-12x^2+2x-2$

Now, equate this to -2, and you will have 2 roots, one of which allows you to find by substitution into the original cubic and tangent line the value of d (when you equate the two as they must have the same value where they touch) and then use the x-value also in your expression for c to find its value.
 
  • #7
MarkFL said:
Yes, after substituting for c, then taking the derivative, you have found:

$\displaystyle y'=-12x^2+2x-2$

Now, equate this to -2, and you will have 2 roots, one of which allows you to find by substitution into the original cubic and tangent line the value of d (when you equate the two as they must have the same value where they touch) and then use the x-value also in your expression for c to find its value.

My teacher said that this is just an exercise concept.
knowing that the derivative in point is the gradient of the tangent line
And he give the equation("2y+4x-6=0") of one of tangent line in some point.
The answer is: m(x)= -2...
 
  • #8
I assumed your teacher wanted you to find a tangent point (0,3), and the values of c and d, which are -2 and 3 respectively.

Here is a plot:
 

Attachments

  • cubicandtangent.jpg
    cubicandtangent.jpg
    11.3 KB · Views: 43
  • #9
MarkFL said:
I assumed your teacher wanted you to find a tangent point (0,3), and the values of c and d, which are -2 and 3 respectively.

Here is a plot:

Every body thought that, thanks for the help MarkFL.
 
  • #10
Glad to help, I found the problem to be interesting, even if I did interpret it incorrectly! :)
 

FAQ: Solving for Derivative of 2x^3-x^2+cx+d

What is the process for solving for the derivative of 2x^3-x^2+cx+d?

The process for solving for the derivative of a polynomial function such as 2x^3-x^2+cx+d is to use the power rule, which states that the derivative of a term with a variable raised to a power is equal to that power multiplied by the coefficient, and the variable raised to one less power. So in this case, the derivative would be 6x^2-2x+c.

What does the variable "c" represent in the polynomial function?

The variable "c" represents the coefficient of the x term in the polynomial function. In this case, it is a constant term and does not change when taking the derivative.

How can the derivative be used to find the slope of the tangent line at a specific point on the graph?

The derivative of a function represents the rate of change of that function at any given point. Therefore, by plugging in the x-coordinate of the desired point into the derivative, the resulting value will give the slope of the tangent line at that point on the graph.

What is the significance of the "d" term in the polynomial function?

The "d" term, also known as the constant term, represents the y-intercept of the polynomial function. It does not have any effect on the derivative as it is a constant value.

Can the derivative of a polynomial function be used to determine the concavity of the graph?

Yes, the second derivative of a polynomial function can be used to determine the concavity of the graph. If the second derivative is positive, the graph is concave up, and if it is negative, the graph is concave down. The point at which the second derivative equals zero is known as an inflection point, where the concavity changes on the graph.

Similar threads

I Partial derivatives of the function f(x,y)
Replies
6
Views
2K
MHB Q1 Can you pass this 3 question AP calculus Quiz in 10 minutes
Replies
3
Views
942
MHB How to Perform Implicit Differentiation on \(x^2-4xy+y^2=4\)?
Replies
1
Views
1K
B Confusion on Implicit Differentiation
Replies
16
Views
2K
MHB How to Find the Second Derivative with Given Equation at a Specific Point?
Replies
1
Views
1K
MHB Solving for d^2y/dt^2: Finding d^2y/dt^2 with dx/dt=1/2
Replies
1
Views
4K
MHB Find the equation of the tangent and normal to.
Replies
4
Views
2K
MHB How Does the Derivative of a Cubic Function Result in a Tangent Line?
Replies
4
Views
3K
MHB Finding k for x is undefined at $x=2$
Replies
3
Views
959
MHB Equation of Normal to Curve at (1,5): Solved?
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top