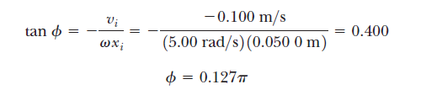Solving for φ on an oscillation problem

[indefiniteintegral]

Homework Statement

A 200-g block connected to a light spring for which the force constant is 5.00 N/m is free to oscillate on a horizontal, frictionless surface. The block is displaced 5.00 cm from equilibrium and has an initial velocity of vi = -0.100 m/s. Find max velocity.

Relevant Equations

tanφ = 0.4

position and velocity expressions for the initial conditions
1) x(0)=Acosφ = xi
2) v(0)=-ωAsinφ= vi

Dividing 2nd equation by equation results in:
-ωAsinφ/Acosφ = xi/vi
tanφ = xi/(-ωvi)
tanφ = 0.4

And here they (the textbook) got φ = 0.127π, This is where I need help please and thank you.

When I see tanφ = 0.4 in order to solve for φ, I would take the arctan of both sides.
That would give me φ = arctan(0.4) = 21.80140949°

Now to actually finish the problem I can find the amplitude by using cos(21.80140949°)
i.e. A = xi/cosφ = 0.05m/cos(21.80140949°) = 0.54m
and I can therefore find the max speed by doing:
vmax = ωA = (5rad/s)(0.54m) = 2.7 m/s

I don't understand how 0.127π was acquired. Going back to:
φ = arctan(0.4) = 21.80140949°

If I want to turn this degree into rad, then I multiple by π/180
φ = 21.80140949(π/180) = (21.80140949/180)π = 0.12111894π

Which obviously 0.12111894π =/= 0.127π

So even though I can still get the right answer for the actual question by using my cosφ, I don't understand how the textbook got their answer of what φ is. Any help would be appreciated please and thank you.

 

[Delta2]

Hmm, this got me into spinning around in 360 deg or should I say $2\pi$ rad.

Indeed it seems to be $\phi=0.121\pi$. Probably a typo in book (that 7 meant to be 1) or some sort of rounding error.

Btw , you seem to have made two typos too, you should have $$\frac{\omega A\sin\phi}{A\cos\phi}=\frac{v_i}{x_i}$$ and $$\tan\phi=\frac{v_i}{\omega x_i}$$.

And I also made a typo in the above lol, I forgot a minus sign.

 

[Delta2]

The book has a typo regarding the minus sign too.

 

[haruspex]

The book has a typo regarding the minus sign too.

Where?

 

[Delta2]

er sorry, the minus before the final result for $\tan\phi$ shouldnt be there, since the initial velocity is given as minus. it is -(-0.1)=0.1

 

[Delta2]

oops no there are two minus ehehe my fault sadge.

 

[haruspex]

oops no there are two minus ehehe my fault sadge.

ok.

But there is a confusing typo in post #1:

1) x(0)=Acosφ = xi​

2) v(0)=-ωAsinφ= vi​

Dividing 2nd equation by equation results in:​

-ωAsinφ/Acosφ = xi/vi (*)​

tanφ = xi/(-ωvi) (*)​

tanφ = 0.4​

In the two equations I have starred, the division on the RHS has been inverted. The final line is correct.

 

[Delta2]

@haruspex you agree that it indeed should be $0.121\pi$ right?

The only way I can see for $0.127\pi$ to happen is if we take the very raw approximation of $\pi$ as 3.1

 

[haruspex]

@haruspex you agree that it indeed should be $0.121\pi$ right?

The only way I can see for $0.127\pi$ to happen is if we take the very raw approximation of $\pi$ as 3.1

Why find the angle at all?
$v_{max}=\omega x_i\sec(\phi)=\omega x_i\sqrt{1+\tan^2(\phi)}=(5)(0.05)\sqrt{1.16}=0.27$.

… which made me check this line:

0.05m/cos(21.80140949°) = 0.54m

Should be 0.054m, no?

 

[Delta2]

Yes ok I guess we don't need to find the phase if we want to find the maximum velocity, but I guess this problem stated here is a sub problem from the complete problem in the book where the complete problem asks for the phase too.

 

[haruspex]

The only way I can see for 0.127π to happen is if we take the very raw approximation of π as 3.1

No, that doesn't make 0.127π right; it only means that the error (0.127 instead of 0.121) is slightly ameliorated by a second error. Slightly, because 0.127 is 6% over whereas 3.1 is only 1% under.
But it makes barely any difference to the max velocity because the amplitude is not much more than 0.05m anyway.

 

[indefiniteintegral]

Why find the angle at all?
$v_{max}=\omega x_i\sec(\phi)=\omega x_i\sqrt{1+\tan^2(\phi)}=(5)(0.05)\sqrt{1.16}=0.27$.

… which made me check this line:

Should be 0.054m, no?

You are hundred percent correct, there were a few typos, it should have been 0.054m and also I did mix up the right hand side of the equation, it should have been vi/xi my apologies! I was running late and trying to get my post down quickly.

I have never seen that formula for max velocity. I'm taking a first year university class in waves and modern physics and its just a prerequisite for my degree - I am not a physics major.

The max formula we have in our book is vmax = ωA, that is the only one I know as of now.

However, when you use vmax = ωxisec(φ) to find the max velocity, my textbook says
"The constant angle φ is called the phase constant (or initial phase angle)"

So when you say, why find the angle at all, aren't you using the very same phase angle that you're saying "why find at all" when you put 21.8°into the equation vmax = ωxisec(φ)? Or what angle do you consider it to be if not the phase angle? (Also I did notice the trig identity you used to get sqrt(1+tan^2x))

My apologies for my novice understanding and if this is a dumb question, this is my first week working with simple harmonic motion, I was suppose to cover it in the mechanics class I did last semester but we just never did. And the class I am on starts on Waves, so this is actually the chapter preceding Waves I am working on (oscillatory motion)

Yes ok I guess we don't need to find the phase if we want to find the maximum velocity, but I guess this problem stated here is a sub problem from the complete problem in the book where the complete problem asks for the phase too.

This is correct (I think?), the problem in full is a) find the period, b) find max speed c) find max accel d) express position, velocity, and acceleration as functions of time e) What if the block were released from the same initial position, xi= 5.00 cm, but with an initial velocity of vi=-0.100 m/s? Which parts of the solution change and what are the new answers for those that do change?So I was trying to understand where the 0.127π came from because when you write the block as a function of time for part e, the φ that is given from earlier in the question is in the equation for the phase constant
ex. x = 0.054cos(5.00t + 0.127π)
So my worry was do I write it as
x= 0.054cos(5.00t + 21.8°), (because I could not figure out how to get 0.127π)
I honestly do not know if writing it like this (with the degree) is acceptable, or if I have to write it in terms of π. Do y'all have any insights as to this?

But I would like to thank you both kindly for your insight and comments its GREATLY appreciated, I spent about an hour trying to figure out a way to get 0.127π, so at least I am not crazy... yet. Thank you for confirming that there is no way in this problem to get that result.

 

[haruspex]

The max formula we have in our book is vmax = ωA,

Yes, and $x(t)=A\cos(\omega t+\phi)$, so here $A=x_i\sec(\phi)$.

So when you say, why find the angle at all, aren't you using the very same phase angle that you're saying "why find at all" when you put 21.8°into the equation vmax = ωxisec(φ)?

We know $\tan(\phi)$ and need $\sec(\phi)$. We do not need the numerical value of the angle to find $v_{max}$, and avoiding that step saves both effort and loss of precision.
But maybe part of the question does ask for the angle .

 

[Delta2]

This is correct (I think?), the problem in full is a) find the period, b) find max speed c) find max accel d) express position, velocity, and acceleration as functions of time e) What if the block were released from the same initial position, xi= 5.00 cm, but with an initial velocity of vi=-0.100 m/s? Which parts of the solution change and what are the new answers for those that do change?

Ok so sometimes I guess correctly , this is indeed part of a bigger problem. If we change the initial velocity everything changes except the period, and we need to find the phase angle in order to answer the new d).

 

[kuruman]

To @indefiniteintegral :
With problems that give you non-zero initial position and velocity, it is convenient to write the most general solution of the simple harmonic oscillator equation as
$x(t)=A \cos(\omega t)+B\sin(\omega t)$
in which case the velocity is
$v(t)=-A\omega \sin(\omega t)+B\omega \cos(\omega t)$

It follows that $A=x(0)$ and $B=\dfrac{v(0)}{\omega}$ in which case
$x(t)=x(0) \cos(\omega t)+\dfrac{v(0)}{\omega}\sin(\omega t)$
$v(t)=-x(0)\omega \sin(\omega t)+v(0)\cos(\omega t)$

I leave it up to you to find the maximum value of $v(t)$.
Hint: $C\sin(\omega t+\phi)=(C\cos\phi)\sin(\omega t)+(C\sin\phi)\cos(\omega t).$

 

[Steve4Physics]

The original question only asks for the maximum velocity. This can very easily/quickly be found using conservation of mechanical energy.

I'd urge the OP to try this for themself.

 

[indefiniteintegral]

Yes, and $x(t)=A\cos(\omega t+\phi)$, so here $A=x_i\sec(\phi)$.

We know $\tan(\phi)$ and need $\sec(\phi)$. We do not need the numerical value of the angle to find $v_{max}$, and avoiding that step saves both effort and loss of precision.
But maybe part of the question does ask for the angle .

Ahhh okay I got you, thank you so much!

 

[indefiniteintegral]

To @indefiniteintegral :
With problems that give you non-zero initial position and velocity, it is convenient to write the most general solution of the simple harmonic oscillator equation as
$x(t)=A \cos(\omega t)+B\sin(\omega t)$
in which case the velocity is
$v(t)=-A\omega \sin(\omega t)+B\omega \cos(\omega t)$

It follows that $A=x(0)$ and $B=\dfrac{v(0)}{\omega}$ in which case
$x(t)=x(0) \cos(\omega t)+\dfrac{v(0)}{\omega}\sin(\omega t)$
$v(t)=-x(0)\omega \sin(\omega t)+v(0)\cos(\omega t)$

I leave it up to you to find the maximum value of $v(t)$.
Hint: $C\sin(\omega t+\phi)=(C\cos\phi)\sin(\omega t)+(C\sin\phi)\cos(\omega t).$

thank you for the suggestion I will keep the general solution in mind when doing further problems!