Solving for Speed & Revolution: F * delta t = p

[Justforthisquestion1]

Homework Statement

I am looking for the distance x from the center of mass of a rod with I(cm) = 1/12 * m * l^2 were i can apply a Force F over a time delta t so that the rod does excactly one revolution before he is back at its original height.

Relevant Equations

Torque, Rotational Energy, Kinetic Energy, angular momentum

Honestly i have very little idea.
F * delta t = p
F * delta t /m = v
So i know the speed of the rod
And i know that however high the rod is supposed to go, when its back down it should have done excactly one revolution.
I have the feeling that I should
So probably i have to use something like
1/2 *a * T^2 = h
and
omega * T = pi?

 

[jbriggs444]

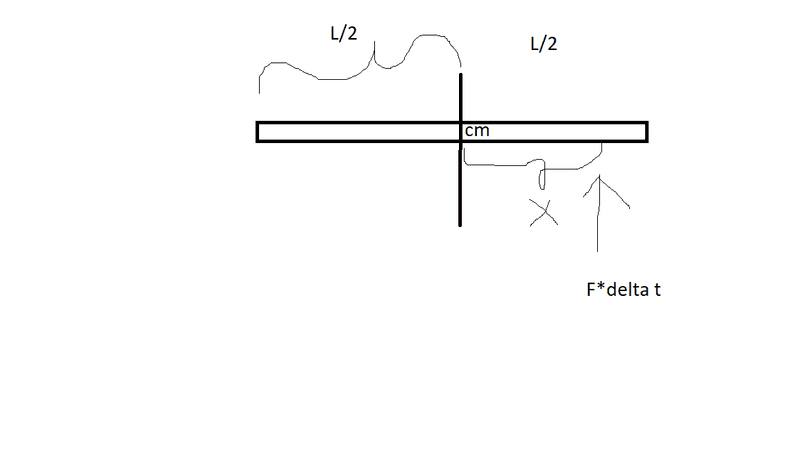
F * delta t = p
F * delta t /m = v
So i know the speed of the rod
[...]
So probably i have to use something like
1/2 *a * T^2 = h

You certainly have enough information that you can know the speed of the rod after the initial force has been applied. With the initial upward velocity in hand, you will be in a position to work on determining the time of flight.

Can you show us the value you arrive at for $v$?

Will the force of gravity during the initial acceleration affect this in any way?

Note that I approve of an approach where you decide on strategy first -- deciding what you can solve for and what that will then allow you to solve for next. With such a strategy in hand, you can proceed to the grunt work of solving the equations.

 

[kuruman]

You certainly have enough information that you can know the speed of the rod after the initial force has been applied.

Did you mean the speed of the rod's center of mass?

To @Justforthisquestion1 : You also have enough information to find the angular speed of the rod as a function of $x$ in terms of F(Δt).

 

[Justforthisquestion1]

Thank you for both your answers!
I think what a dont understand is, is whether the point of force application has to be included when calculating v or omega. Also the body will translate and rotate which confuses me even more.
So lets say:
F*delta t = m * v
--> v = F * delta t / m
and since i apply F at distance x from cm it should be
omega = F *delta t / (m * x)
Is that correct so far? The force has to cause translation as well as rotation?

Edit no wait i have to use angular momentum dont i?
r * p = I * omega
with p = F * delta t
an I = 1/12 * m * l^2
we get:
omega = 12 * x * F * delta t / (m * l^2)
and then i would get the speed of cm by multiplying omega with l? Or do i use F * delta t = m * v
for v of cm? And why?

 

[haruspex]

since i apply F at distance x from cm it should be
omega = F *delta t / (m * x)

No, you have to consider the moment of inertia of the rod.
What angular momentum will the force impart to the rod?

 

[Justforthisquestion1]

No, you have to consider the moment of inertia of the rod.
What angular momentum will the force impart to the rod?

Thats kind of a tricky question.
i am using the cm as axis of rotation?
x * p = angular momentum?
-->
x * p = l * omega
with p = F * delta t
an I = 1/12 * m * l^2
we get:
omega = 12 * x * F * delta t / (m * l^2)
and then i would get the speed of cm by multiplying omega with l? Or do i use F * delta t = m * v
for v of cm? And why?

 

[Justforthisquestion1]

No!
I had it all wrong. So angular momentum and linear momentum are conserved separately.
So for v and the conservation of linear momentum i can say
p = m * v
--> F * delta t / m = v
But for omega and the conservation of angular momentum i can say
p * x = I * omega
omega = p * x / I

Edit: Okay so now i am stuck again. I now now v and omega.
And as i said before i have a time T in which the stich rises up and falls down again, and does exactly one revolution.
So omega * T = 2 * pi
and 0.5 * m * v^2 = m * g * h
But how to go on?

 

[Justforthisquestion1]

You certainly have enough information that you can know the speed of the rod after the initial force has been applied. With the initial upward velocity in hand, you will be in a position to work on determining the time of flight.

Can you show us the value you arrive at for $v$?

Will the force of gravity during the initial acceleration affect this in any way?

Note that I approve of an approach where you decide on strategy first -- deciding what you can solve for and what that will then allow you to solve for next. With such a strategy in hand, you can proceed to the grunt work of solving the equations.

Gravity is to be neglected during the initial acceleration
For the rest please kindly look to my entry before this one

 

[haruspex]

omega = 12 * x * F * delta t / (m * l^2)

good

and then i would get the speed of cm by multiplying omega with l?

No. ω is the rate of rotation about the cm.
You already have the speed of the cm:

F*delta t = m * v

 

[Justforthisquestion1]

good

No. ω is the rate of rotation about the cm.
You already have the speed of the cm:

Yes because angular momentum and linear momentum are conserved separately.
Now:
i have a time T in which the rod rises up and falls down again, and does exactly one revolution.
So omega * T = 2 * pi
and 0.5 * m * v^2 = m * g * h
and also v * t - 0.5 * g *T^2 = 2* h
This is because it needs to go up and down so 2 * h
Oh i just realized i can combine these 3! I will be back in a bit when i have calculated it

 

[Justforthisquestion1]

Does gravity produce torque around the cm? It should not?

 

[haruspex]

Does gravity produce torque around the cm? It should not?

Right, it does not. In fact, that's almost the definition of cm.

 

[erobz]

@Justforthisquestion1

Please see the Latex Math formatting guide. It will help you convey you work, and help others interpret it. It's not laborious to learn the basics.

 

[Justforthisquestion1]

@Justforthisquestion1

Please see the Latex Math formatting guide. It will help you convey you work, and help others interpret it. It's not laborious to learn the basics.

Will do