Solving for the components of a force at a given angle on a plane.

[mathmari]

Hey!

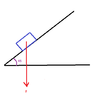
We suppose that a force $\overrightarrow{F}$ (for example, the gravity) is applied vertically downwards to an object that is placed at a plane which has an angle of $45^{\circ}$ with the horizantal direction.
Express this force as a sum of a force that acts parallel to the plan and of a force that acts perpendicular to that.

Do we have the following??

View attachment 4035

To write the force as the sum of a force that acts parallel to the plan and of a force that acts perpendicular to that, do we have to write the components of the force at the $x-$axis and at the $y-$axis?? (Wondering)

 

[mathmari]

To write the force as a sum of its component, we have the following:

$$F_x=F \frac{\sqrt{2}}{2} \\ F_y=F \frac{\sqrt{2}}{2}$$

The result should be $$\overrightarrow{F}_x=\frac{F}{2}(-\overrightarrow{i}-\overrightarrow{j}) \\ \overrightarrow{F}_y=\frac{F}{2}(\overrightarrow{i}-\overrightarrow{j})$$

How do we get it?? (Wondering)

 

[mathmari]

To write the force as a sum of its component, we have the following:

$$F_x=F \frac{\sqrt{2}}{2} \\ F_y=F \frac{\sqrt{2}}{2}$$

Do we maybe have to do the following?? (Wondering)

$$\overrightarrow{F}_x=A\overrightarrow{i}+B\overrightarrow{j} \Rightarrow F_x=\sqrt{A^2+B^2}\\ \overrightarrow{F}_y=C\overrightarrow{i}+D\overrightarrow{j} \Rightarrow F_y=\sqrt{C^2+D^2}$$

$$\sqrt{A^2+B^2}=F\frac{\sqrt{2}}{2} \\ \sqrt{C^2+D^2}=F\frac{\sqrt{2}}{2}$$

But we have only $2$ equations and $4$ unkown variables...

Is this correct so far?? (Wondering)

 

[I like Serena]

To write the force as the sum of a force that acts parallel to the plan and of a force that acts perpendicular to that, do we have to write the components of the force at the $x-$axis and at the $y-$axis?? (Wondering)

That depends on how you pick your $x-$axis and $y-$axis.
Usually those are horizontal respectively vertical.
I'd say you need the components $F_\parallel$ and $F_\perp$ to avoid ambiguity. (Mmm)

Do we maybe have to do the following?? (Wondering)

$$\overrightarrow{F}_x=A\overrightarrow{i}+B\overrightarrow{j} \Rightarrow F_x=\sqrt{A^2+B^2}\\ \overrightarrow{F}_y=C\overrightarrow{i}+D\overrightarrow{j} \Rightarrow F_y=\sqrt{C^2+D^2}$$

$$\sqrt{A^2+B^2}=F\frac{\sqrt{2}}{2} \\ \sqrt{C^2+D^2}=F\frac{\sqrt{2}}{2}$$

But we have only $2$ equations and $4$ unkown variables...

Is this correct so far?? (Wondering)

It's correct, but you didn't use the angle of 45 degrees yet... (Thinking)

 

[mathmari]

It's correct, but you didn't use the angle of 45 degrees yet... (Thinking)

What do you mean?? (Wondering) I got stuck right now...

 

[I like Serena]

What do you mean?? (Wondering) I got stuck right now...

Any vector can be written as the sum of 2 vectors.
In this case we want to write a vertical vector $\overrightarrow F = F \mathbf{\hat k}$ as the sum of a vector that is parallel to the surface ($F_\parallel$) and a vector that is perpendicular to the surface ($F_\perp$). In particular, they are perpendicular with respect to each other.
Since the surface is at a 45 degree angle, due to symmetry, those two vectors will have the same length.
So $F_\parallel = F_\perp$ and using Pythagoras: $F_\parallel^2 + F_\perp^2 = F^2$.

Care to solve that? (Wondering)