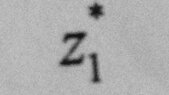fordy2707
- 24
- 0
hi all,hope I find you all well and that I've posted this in the correct section
ive been given this $z_1$ =1-j2
Question ,find and show the result of $z_1 ^*$ on an argand diagram ,my question is what does the star symbol represent or is it a typo?
many thanks
ive been given this $z_1$ =1-j2
Question ,find and show the result of $z_1 ^*$ on an argand diagram ,my question is what does the star symbol represent or is it a typo?
many thanks