- #1
David112234
- 105
- 3
Lets consider a hollow sphere with charge +q and than a larger hollow sphere that encloses it with -q, so two spheres one inside the other. Now we use draw an even larger Gaussian sphere that encloses both of these,
∫EdA = Qinclosed/ ∈_0
the total enclosed charge is +q + -q = 0
so
∫EdA = 0
E ∫dA = E (area of sphere) =0
so the Electric field must be zero, but how could that be? So any test charge (black square in diagram) placed outside the two sphere will experience absolutely no electric force? Wouldn't it experience some force from the -q sphere since it is on the outside and always closer to any test charge?
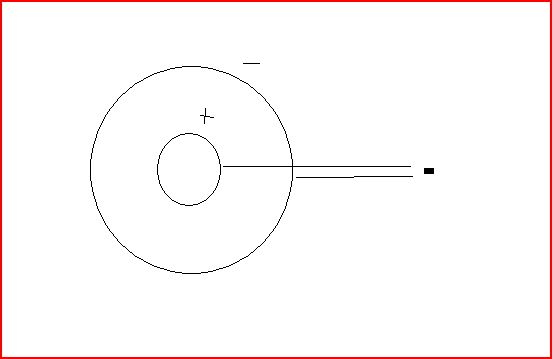
∫EdA = Qinclosed/ ∈_0
the total enclosed charge is +q + -q = 0
so
∫EdA = 0
E ∫dA = E (area of sphere) =0
so the Electric field must be zero, but how could that be? So any test charge (black square in diagram) placed outside the two sphere will experience absolutely no electric force? Wouldn't it experience some force from the -q sphere since it is on the outside and always closer to any test charge?