Solving Geodesic Equations for ##\phi(r)##

[davidge]

The system of DE

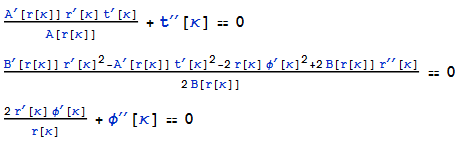
arises when using the Schwarzschild metric of General Relativity on the geodesics equation. I was trying to solve these equations for $\phi$ as a function of $r$. I followed Weinberg (Weinberg's book S&G relativity) who uses $t' = 1 / B(r)$ in his book. So now we have two equations and two unkowns. I tried to solve it for $\phi (r)$ as I said above but Mathematica keeps running indefinitely and gives no solution. I was hoping to get the same result as Weinberg does in his book. What am I doing wrong?

 

[Ambitwistor]

First of all, let me commend you for delving into the complex and fascinating world of General Relativity. Solving the equations for $\phi$ as a function of $r$ can be a challenging task, especially when using the Schwarzschild metric.

One possible reason for Mathematica running indefinitely and not giving a solution could be that the equations you are trying to solve are non-linear and cannot be easily solved analytically. In such cases, numerical methods may be necessary to obtain a solution.

Another possibility is that there may be an error in your code or in the equations themselves. It is always a good idea to double-check your work and make sure all the equations and variables are correctly entered.

Additionally, it is important to keep in mind that the Schwarzschild metric is a solution to the Einstein field equations in vacuum, meaning that it does not take into account the presence of matter or energy. This may also affect the results you are obtaining.

I would suggest consulting with a colleague or seeking help from a mentor or expert in the field to review your work and offer guidance. It may also be helpful to try different methods or approaches to solving the equations.

In any case, do not be discouraged if you are not getting the same result as Weinberg does in his book. General Relativity is a complex and ever-evolving theory, and there may be multiple valid solutions to the equations. Keep exploring and learning, and you may uncover new insights and discoveries.