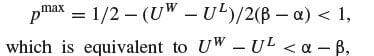Solving Inequality: Get Help with (Uw-UL)<a-B

[martyfarty]

Hi, I am reading a paper and in this equation is given.

View attachment 6477

I don't quite follow how they end up with the last (Uw-UL)<a-B. If I do it myself I get the inequality sign wrong.

Any help?

Thx

 

[Euge]

Welcome martyfarty,

The inequality holds if and only if $\alpha > \beta$. If you had the inequality reversed, then perhaps you had $\alpha < \beta$.

 

[martyfarty]

Indeed \alpha > \beta is true. How would you step by step come to the last equation given that \alpha > \beta?

 

[MarkFL]

Let's first subtract $$\frac{1}{2}$$ from both sides:

$$\frac{\left(U^W-U^L\right)}{2(\alpha-\beta)}<\frac{1}{2}$$

If $\alpha-\beta>0$, then we may multiply through by $2(\alpha-\beta)$ to get:

$$U^W-U^L<\alpha-\beta$$

 

[martyfarty]

Let's first subtract $$\frac{1}{2}$$ from both sides:

$$\frac{\left(U^W-U^L\right)}{2(\alpha-\beta)}<\frac{1}{2}$$

If $\alpha-\beta>0$, then we may multiply through by $2(\alpha-\beta)$ to get:

$$U^W-U^L<\alpha-\beta$$

However, $$\alpha$$ and $$\beta$$ are reversed right? Like this

$$\frac{\left(U^W-U^L\right)}{2(\beta-\alpha)}<\frac{1}{2}$$

 

[MarkFL]

However, $$\alpha$$ and $$\beta$$ are reversed right? Like this

$$\frac{\left(U^W-U^L\right)}{2(\beta-\alpha)}<\frac{1}{2}$$

No, I reversed them to get rid of the leading negative for that term. :D

 

[martyfarty]

No, I reversed them to get rid of the leading negative for that term. :D

Okay wow, that option did not even cross my mind haha. Thanks for your help!