Solving Infinite Square Well: Eigen Functions & Solutions

[mr_whisk]

Hi all,

Sorry if this question is not very challenging, but I am driving myself to confusion...

I happily derived the eigen functions for an infinite square well spanning from 0 to L and found them to be:

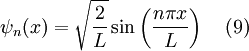
...in agreement with wikipedia.

However my course notes derive solutions for an inf sq well between -a and +a.

Surely L=2a, no?

In the notes n=1,3,5... produces cosine solutions and n=2,4,6... produce sine solutions.

Why is there now cosine solutions?

Please help, I'm going crazy :)

 

[dx]

You can get the solutions on [-L/2 , L/2] from the solutions on [0, L] by replacing x by x + L/2 (i.e. moving the solutions to the left by L/2). For example, sin(πx/L) becomes sin((π/L)(x + L/2)) = sin(πx/L + π/2) = cos(πx/L).

 

[mr_whisk]

Thankyou dx,

That's brilliant, it all makes sense :)

 

[jtbell]

Draw a graph of the ground state (n = 1) solution for both cases. You'll see that the two graphs are identical except for the origin (x = 0) being in different places relative to the walls of the well. Likewise for n = 2, etc.