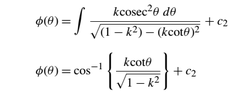Solving Integral in Picture: Step-by-Step Guide

In summary, the conversation discusses possible solutions for an integral involving trigonometric functions and the substitution method. The suggested substitution is $\cot(\theta)=\frac{\sqrt{1-k^2}}{k}\cos(u)$ and the resulting solution is $\phi=-\sin^{-1}(\frac{k\cot(\theta)}{\sqrt{1-k^2}})+C$. However, it is noted that another possible form is $\phi=\cos^{-1}(\frac{k\cot(\theta)}{\sqrt{1-k^2}})+C$, which can be derived from the identity $\sin^{-1}(x)+\cos^{-1}(x)=\frac{\pi}{2}$ and the fact that the sum of
  • #1
FilipVz
8
0
View attachment 1922

Can somebody explain how to solve integral from the picture above?( solution is in the second line)
 

Attachments

  • Integral.png
    Integral.png
    4.3 KB · Views: 75
Physics news on Phys.org
  • #2
I haven't worked out the solution yet, but given the answer and the general form of the integral I would guess trig substitution is the way to solve it. Question though - should the $(1-k^2)$ in the denominator actually be $(1-k^2)^2$?

If that's not the way to solve it then maybe there's something with the substitution $(k \cot(\theta))^2=k^2 \cot^2(\theta)=k^2(\csc^2(\theta)-1)$, but I'm not sure yet. Will post back if anything comes to mind.
 
  • #3
Hint :

\(\displaystyle \frac{d}{dx} \left(\cos^{-1} (f) \right) = \frac{-f'}{\sqrt{1-f^2}}\)​
 
  • #4
Hint: Try the substitution:

\(\displaystyle \cot(\theta)=\frac{\sqrt{1-k^2}}{k}\cos(u)\)

Hence:

\(\displaystyle \csc^2(\theta)\,d\theta=\frac{\sqrt{1-k^2}}{k}\sin(u)\,du\)

And the result will follow. :D
 
  • #5
MarkFL said:
Hint: Try the substitution:

\(\displaystyle \cot(\theta)=\frac{\sqrt{1-k^2}}{k}\cos(u)\)

Hence:

\(\displaystyle \csc^2(\theta)\,d\theta=\frac{\sqrt{1-k^2}}{k}\sin(u)\,du\)

And the result will follow. :D

No need for substitution. Of course it is more advisable on an elementary level .
 
  • #6
Thank you,

i solved it, using substitution:

\(\displaystyle u= (k*ctgθ)/(1-k^2 )\)

But, my result is:

\(\displaystyle ϕ=-arcsin((k∙ctgθ)/√(1-k^2 ))+c_2\)

instead of

\(\displaystyle ϕ=arccos((k∙ctgθ)/√(1-k^2 ))+c_2\)

Is this correct?
 
  • #7
FilipVz said:
Thank you,

i solved it, using substitution:

\(\displaystyle u= (k*ctgθ)/(1-k^2 )\)

But, my result is:

\(\displaystyle ϕ=-arcsin((k∙ctgθ)/√(1-k^2 ))+c_2\)

instead of

\(\displaystyle ϕ=arccos((k∙ctgθ)/√(1-k^2 ))+c_2\)

Is this correct?

Yes, that's another possible form. Consider the identity:

\(\displaystyle \sin^{-1}(x)+\cos^{-1}(x)=\frac{\pi}{2}\)

along with the fact that the sum of an arbitrary constant and another constant is still an arbitrary constant. :D
 
  • #8
\(\displaystyle \int \frac{-1}{\sqrt{1-x^2}} \, dx = \cos^{-1}(x)+A\)

\(\displaystyle -\int \frac{1}{\sqrt{1-x^2}} \, dx = -\sin^{-1}(x)+B\)

And this simply because

\(\displaystyle \cos^{-1}(x)+\sin^{-1}(x) =\frac{\pi}{2}\)
 

FAQ: Solving Integral in Picture: Step-by-Step Guide

1. How do I solve an integral using a picture?

To solve an integral using a picture, you need to first determine the bounds of integration and the function being integrated. Then, you can graph the function and the area under the curve. Next, you can use geometric shapes to estimate the area and break it down into smaller, easier to solve integrals. Finally, you can use the fundamental theorem of calculus to find the exact value of the integral.

2. What is the fundamental theorem of calculus?

The fundamental theorem of calculus states that the definite integral of a function f(x) can be evaluated by finding the antiderivative of f(x) and evaluating it at the upper and lower bounds of integration. In other words, it relates differentiation and integration by showing that integration is the inverse operation of differentiation.

3. Can I use a picture to solve any type of integral?

No, using a picture to solve integrals is most effective for finding the area under a curve for continuous functions. It may not work for more complex integrals involving trigonometric, logarithmic, or exponential functions.

4. How accurate is solving an integral using a picture?

Using a picture to solve integrals is not always accurate and is more of an estimation method. The accuracy depends on the precision of the graph and the geometric shapes used to estimate the area. It is recommended to use other methods, such as the fundamental theorem of calculus, for more precise results.

5. Are there any limitations to solving integrals using a picture?

Yes, there are some limitations to using a picture to solve integrals. It may not work for all types of functions and can be time-consuming and error-prone. Also, it may not be feasible to use this method for more complex integrals with multiple variables or in higher dimensions.

Similar threads

B Integration by parts of inverse sine, a solved exercise, some doubts...
Replies
4
Views
2K
A Integration of trigonometric functions
Replies
4
Views
2K
I Solving an Integral using Feyman's trick
Replies
8
Views
1K
MHB How Do You Solve an Integral with Two Variables?
Replies
5
Views
1K
I Why is this closed line integral zero?
Replies
8
Views
2K
Solution to ∫ dx x^2 /(1+x^2): Step-by-Step Guide
Replies
4
Views
7K
I Can Differentiating a Simple Fraction Simplify Complex Integration?
Replies
10
Views
1K
MHB Steps for Setting Up Triple Integrals
Replies
4
Views
2K
I Did Math DF's integral calculator make a glaring mistake?
Replies
8
Views
1K
I Is There a Better Way to Solve Integrals Than Symbolab and Mathematica?
Replies
9
Views
3K

Hot Threads

Recent Insights

Back
Top