Solving Laplace Equation in Cylindrical Coordinates - Potential Outside Cylinder

[ricky123]

The potential on the side and the bottom of the cylinder is zero, while the top has a potential V_0. We want to find the potential outside the cylinder.

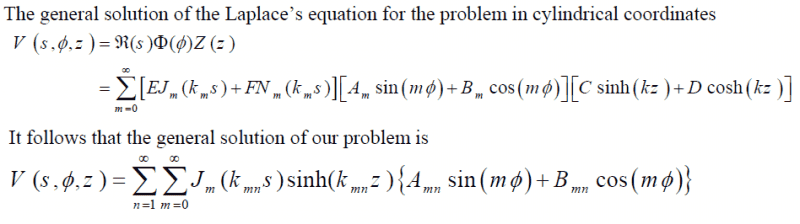
Can I use the same boundary conditions as for case of inside cylinder potential?
What is different?

 

[ShayanJ]

The difference is about the functions used in the expansion. The Js are Bessel functions of the first kind and have no singularity, so there is nothing about them. But there is a point about the Ns. They're called Bessel functions of the second kind, Weber functions or Neumann functions. They have a singularity at the origin and because we want a finite potential everywhere, we don't use the Ns for inside the cylinder. But because outside the cylinder, the Ns are finite too, you can use them in the potential too and don't have to use only Js in the s-dependent part.
Boundary conditions are the same. Just there are two added, the equality of the two potentials (for inside and outside of the cylinder) and their derivatives should be equal at the surface of the cylinder.

 

[ricky123]

Thanks for your reply.
The general solution for potential outside the cylinder is than
\Phi(\rho>a, \varphi, z)=\sum_{m=0}^{\infty}\sum_{n=1}^{\infty}\big(J_{m}(k_{mn}\rho)+N_{m}(k_{mn}\rho)\big)\sinh(k_{mn}z)[A_{mn}\sin(m\varphi)+B_{mn}\cos(m\varphi)].
Is there sin hyp function in z dependence part?
Or must we split function on two part, for z>L and z<L and use exp function for z-dependent part? Because hyp functions don't vanish when z goes to infinity.
\Phi(\rho&gt;a, \varphi, z&gt;L)=\sum_{m=0}^{\infty}\sum_{n=1}^{\infty}\big(J_{m}(k_{mn}\rho)+N_{m}(k_{mn}\rho)\big)\mathrm{e}^{-k_{mn}z}[A_{mn}\sin(m\varphi)+B_{mn}\cos(m\varphi)]
\Phi(\rho&gt;a, \varphi, z&lt;L)=\sum_{m=0}^{\infty}\sum_{n=1}^{\infty}\big(J_{m}(k_{mn}\rho)+N_{m}(k_{mn}\rho)\big)\mathrm{e}^{k_{mn}z}[C_{mn}\sin(m\varphi)+D_{mn}\cos(m\varphi)]
What is the right way?

There is a sketch for a better illustration:

 

[Orodruin]

The difference is about the functions used in the expansion. The Js are Bessel functions of the first kind and have no singularity, so there is nothing about them. But there is a point about the Ns. They're called Bessel functions of the second kind, Weber functions or Neumann functions. They have a singularity at the origin and because we want a finite potential everywhere, we don't use the Ns for inside the cylinder. But because outside the cylinder, the Ns are finite too, you can use them in the potential too and don't have to use only Js in the s-dependent part.
Boundary conditions are the same. Just there are two added, the equality of the two potentials (for inside and outside of the cylinder) and their derivatives should be equal at the surface of the cylinder.

His cylinder is finite and part of the z axis is contained in the outside as well. His boundary conditions are specified on the full cylinder surface and there is no need to add further conditions. There is in general going to be a surface charge in order to fulfill the given boundary conditions, so the potential may not be differentiable on the surface.

Furthermore I suspect this problem will not admit a simple series solution since the outside of the cylinder is a relatively nasty space to work in. The eigenfunctions are going to be fairly nasty and you will probably have to patch solutions in different parts of space with corresponding solutions to match the boundaries.